Graphics, Imaging, and Games Lab

Introduction

In my last few posts, I explored global image recolouration, where I attempted to find some measurement of how "interesting" a pixel's original colour is and assign "uninteresting" pixels a new colour. I intended to insert features of a new image (a solid colour, in most cases), in a manner which did not eliminate the essential features of the original image.

In this post, I am presenting results from local image recolouration. Local recolouration involves blending the source image with a new image only in a specific region.

As the cumulative range geodesic filter is an edge-preserving filter and a reasonably effective texture-preserving filter, local recolouration with cumulative range geodesic filtering could, in theory, be used to either:

1. Show the region of pixels that are "closest" to the source pixel (the starting point for building the recolouration region), by recolouring pixels strictly based on their measure of similarity to the source pixel.
2. Indicate which pixels are "close" to the source pixel by recolouring them, but vary the degree of recolouration within each small area of the region so as to preserve or emphasize texture.

Ideas for Further Experiments

Image recolouration and re-texturing is both a very broad area of investigation and tangential to my main project of developing an image filter. Regarding item "B" above, there are a number of procedures I could try if I devoted more time to local recolouration:

• Weight recolouration by distances to the source pixel, multiplied by some measurement of how extreme a pixel is, such as its value in the residual from filtering (see http://gigl.scs.carleton.ca/node/539), or its count of mask inclusions (see http://gigl.scs.carleton.ca/node/536).
• Segment pixel distance values using the K-means algorithm, for example.
  • Assign a recolouration weight to the mean distance value of each segment.
  • Calculate the degree of recolouration of each pixel as equal to the sum of the recolouration weight assigned to the segment with an offset determined by the deviation of its distance value from the mean distance value of the segment.
  • This should allow for a highly textured recolouration which nevertheless diminishes with the average distance from the source pixel.
• Use the gradient of the distances to the source pixel in some fashion. (In other words, consider the distance to the source pixel as a single-valued function of two pixel coordinates, and calculate the magnitude of gradient of this function to quantify texture in the image.)
  • Perhaps using the image gradient would yield similar results to using the gradient of distance values.

Method

All results in this post were produced by generating a filtering mask for the pixel to be recoloured, using  a mask size equal to the number of pixels in the entire image, and a "gamma" parameter value of zero. I used the normal cumulative range geodesic filter (as described at http://gigl.scs.carleton.ca/node/481) to obtain filtering masks.

Once the filtering mask had been calculated, I extracted some pixel-specific quantity of interest from the mask and linearly scaled this quantity to values covering the full interval of zero to one (including 0 and 1). (In my initial tests, I used the distances of pixels from the source pixel as the values scaled to 0-1.) I will refer to the values between 0 and 1 as the "proto-weights" for recolouration.

In order to modify the appearance of the recoloured image, I applied some kind of transformation (square root, exponential, etc.) to the proto-weights to obtain a new set of values between 0 and 1. These values differ from the proto-weights in that they do not necessarily need to fill the entire interval of [0,1]. However, in this post, all transformations that I used effectively resulted in values in the full range of 0 to 1.

I used two parameters, "minWeight" and "maxWeight", which were both between 0 and 1, to define a new range of values. The transformed proto-weights were scaled linearly to the interval [minWeight, maxWeight]. In other words, values of 0 would be mapped to minWeight, and values of 1 would be mapped to maxWeight. When producing the results shown in this post, I used minWeight = 0 and maxWeight = 1, for simplicity.

The final values in the interval [minWeight, maxWeight] are the recolouration weights. I generated the recoloured image using the following equation:

New pixel colour = (old pixel colour)*(1-weight for this pixel) + (new colour)*(weight for this pixel)

Implementation Notes

I wanted to avoid specifying the coordinates of the source pixels for recolouration in advance of running the program. As the time required to produce a recoloured image was normally on the order of a few seconds, I decided to build a graphical user interface (GUI) for interactive recolouration of an image. This turned out to be an interesting exercise, as I have not previously developed GUIs with MATLAB.

Using some high-level GUI creation functions available in MATLAB's Image Processing Toolbox, I was able to incorporate a scroll panel, navigation window, magnification control, and pixel information tool into the GUI to allow for easy exploration of the image. To recolour the image from a specific source pixel, the user can simply click on the display of the image at the point corresponding to the desired source pixel.

MATLAB Local Image Recolouration GUI

Selecting a basis for recolouration

Source Image

The following images demonstrate the use of different source data for calculating recolouration weights. All images were produced without applying any transformation to the "proto-weight" values. (In other words, the recolouration weights are equal to the proto-weights.) The green marker in each image indicates the location of the source pixel.

Recoloration based on distance to the source pixel

Recolouration based on order of addition to the filtering mask (i.e. "mask index")

Recolouration based on order of (distance to source pixel)*(mask index)

Recolouration based on the base-2 logarithm of downstream counts

Recolouration based on lengths of paths to the source pixel

From the above series of images, it seems that weighting the recolouration process by distances yields the best results.

Transformation of recolouration proto-weights

Evidently, as shown above, most of the types of values used to calculate recolouration weights change too slowly as the spatial separation between the source pixel and the given pixel increases. As a result, the image is more or less globally-recoloured. To solve this problem, I applied nonlinear transformations to the "proto-weights" when calculating weights used for recolouration.

Consider the following series of images, which all use distances to the source pixel as the basis for recolouration. A plot of the corresponding nonlinear transformation function is provided below each image:

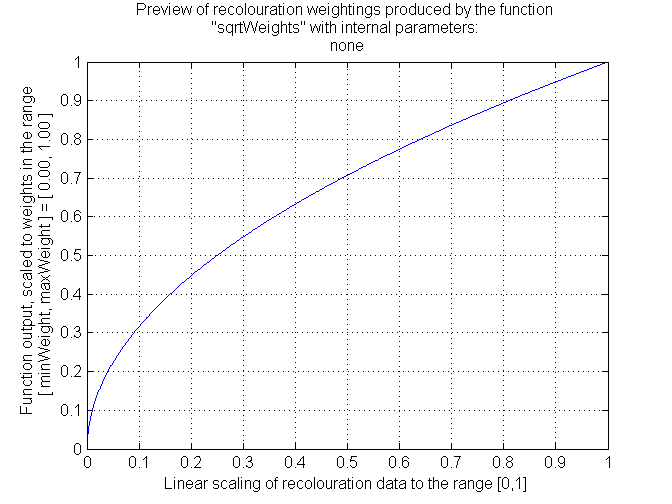
Identity Transformation (Same as the image shown in the previous section)

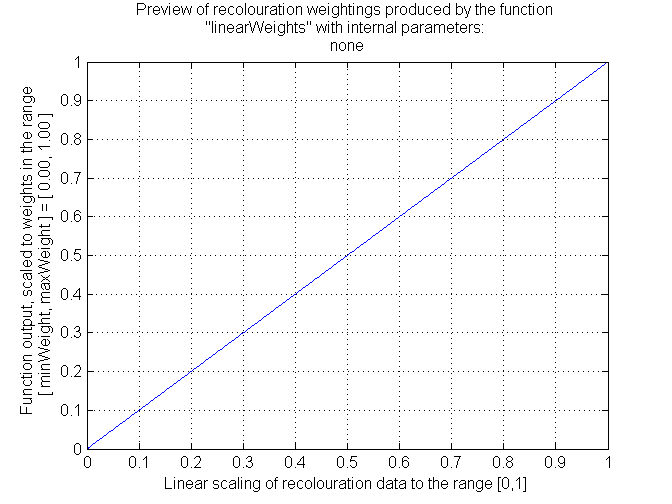
Square Root Transformation

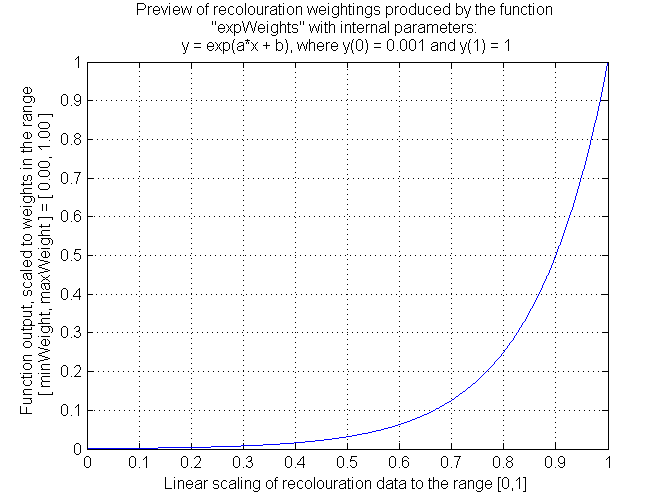
Exponential Transformation

Reciprocal Transformation

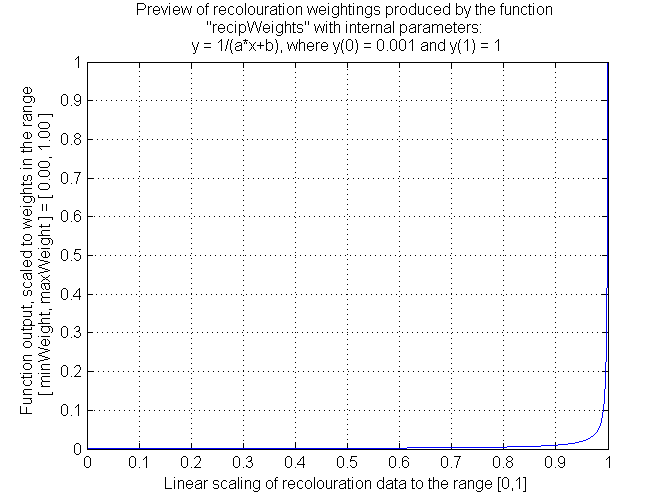
Out of the above series of images, I prefer the recoloured image made using an exponential transformation. The exponential transformation provides the most compact recoloured area that is possible without producing hard edges on the recoloured area (which occurs with the reciprocal transformation).

(Image Source: Bernard Llanos)