Graphics, Imaging, and Games Lab

Motivation

In the near future, I plan to develop a number of variations on the cumulative range geodesic filter, with the intention of building a filter having the following properties:

• Noise pixels in the image (outliers) are strongly smoothed towards neighbouring colours, and neighbouring colours are not contaminated by noise colours. To be specific, noise pixels are pixels whose colours are very different from the colours of their surroundings. Noise pixels do not contribute to the desired texture of the image. The current filter can fail to remove noise for a few reasons:

1. Noise pixels get included in the filtering masks of nearby, normal-coloured pixels. As the filter grows the mask, noise pixels become increasingly likely to be added, since a nearby noise pixel can have the same "cost" as a distant pixel with a colour similar to that of the source pixel.
2. If the source pixel of a filtering mask is a noise pixel, the filtering mask will preferentially include any similar, neighbouring noise pixels. This is a particular concern if noise pixels are scattered close to the edges of regions that have the same colour as the noise pixels.
3. Noise pixels are included in the averages used to determine new pixel colours. In the basic cumulative range geodesic filter, this is equivalent to the first two points in this list, since all pixels included in filtering masks are part of the corresponding averages. However, a new filter could be designed which excludes some mask pixels from the average.

• Protection of local extrema: Pixels which lie at the peaks of local colour variations in the image. These differ from noise pixels in that there are gradual, as opposed to abrupt, colour changes which occur over the extrema and their nearest neighbours. Specular highlights and shadows are examples of local extrema. Flattening of local extrema results in a loss of colour and tonal contrast during filtering.

• Preservation of noise-like textures: Textures such as sand resemble patterns of random noise in low-resolution images. Ideally, the filter should be able to remove sporadic noise, but keep high frequency colour variations when they occur in close proximity. The current version of the cumulative range geodesic filter is unable to preserve sand-like textures (refer to the results at the end of the article at http://gigl.scs.carleton.ca/node/481).

Method

Trying to achieve the goals mentioned above requires some way of evaluating how filters perform according to these criteria. Simply looking at filtered images is effective when comparing two entirely different filtering approaches (e.g. a spatial averaging filter and a bilateral filter), but may not be reliable for comparing variations on a single filtering algorithm. In contrast, a quantitative measurement of filter performance could be a very reliable way to differentiate similar filters, but has the disadvantage of producing comparisons based on either abstracted or very narrow descriptions of images.

My quantitative method for comparing filtering processes is as follows:

• Generate images composed initially of only two colours, arranged in a random pattern, as shown below. The image on the right is a variation on this process which simulates the effect of having noise pixels adjacent to a larger region of the same colour. In practice, I found that the full noise pattern and the half noise pattern yield similar values for the measurements that I chose to calculate.

• Apply a Gaussian filter to the image to blur the noise pattern to some extent. (In the case of the split image, the edge of the solid-coloured region is not blurred, as only the noise pattern half is subject to the Gaussian filtering process.) As the image becomes increasingly blurred, the pattern changes from a pattern of noise to a pattern of local extrema.

• Filter the image. The sample images below compare original images (at the top or left) with their filtered versions (below or to the right). Notice that, in the split image, noise pixels closer to the solid-coloured area are preserved to a greater extent. (Filtering was performed with the normal cumulative range geodesic filter at a mask size of 256 pixels and a gamma parameter value of zero.)

• Finally, I compare the original and filtered images using the following three measurements:

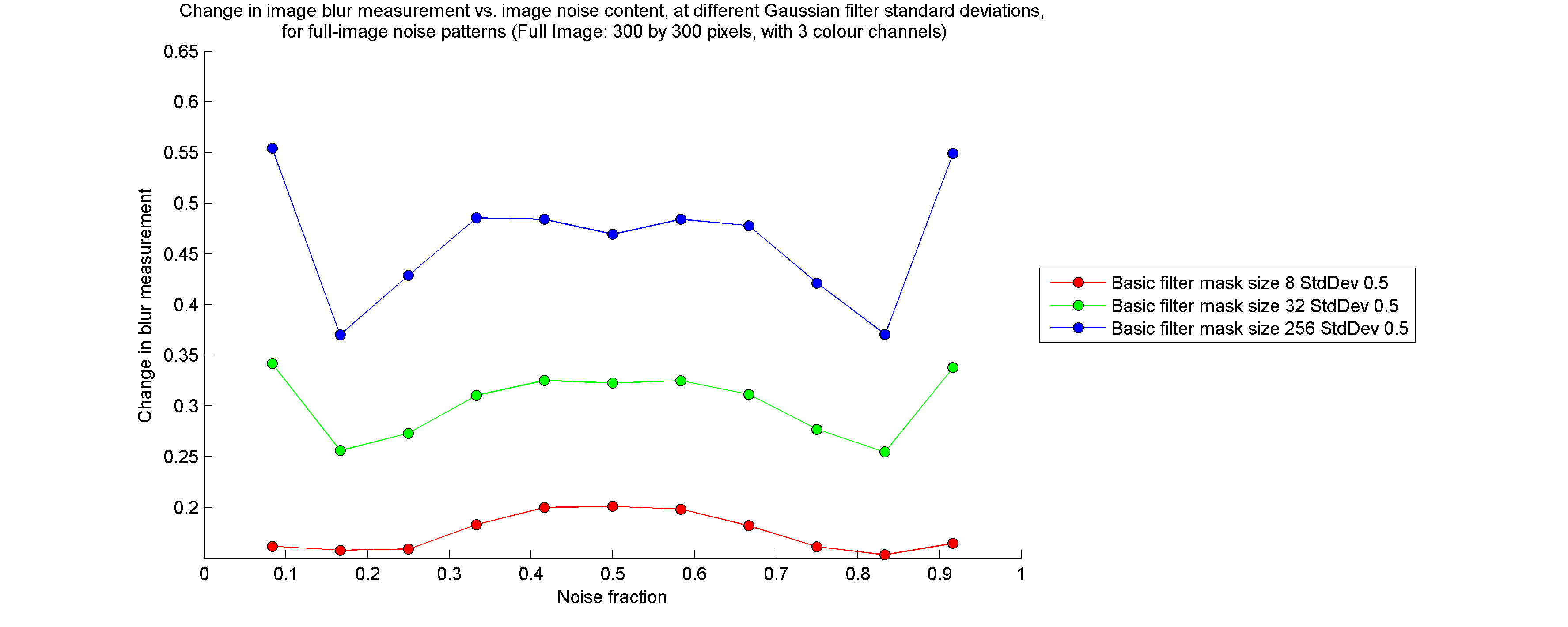
  • Change in "blur": Blur is computed as the average colour difference (length of the average vector difference in RGB space) between a pixel and any of its 4 nearest neighbours. The change in blur is equal to the subtraction of the blur of the filtered image from the blur of the original image, expressed as a fraction of the blur of the original image (i.e. Change in Blur = ( Blur_original - Blur_filtered ) / Blur_original )

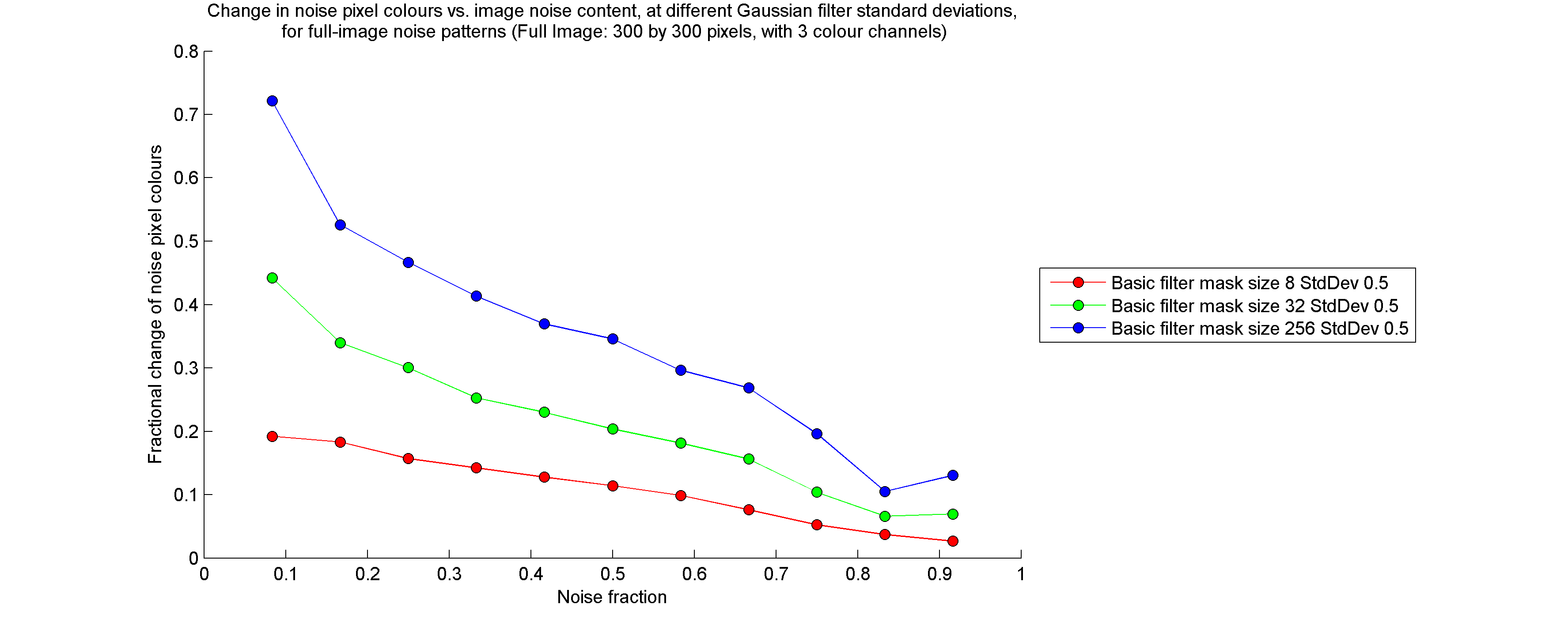
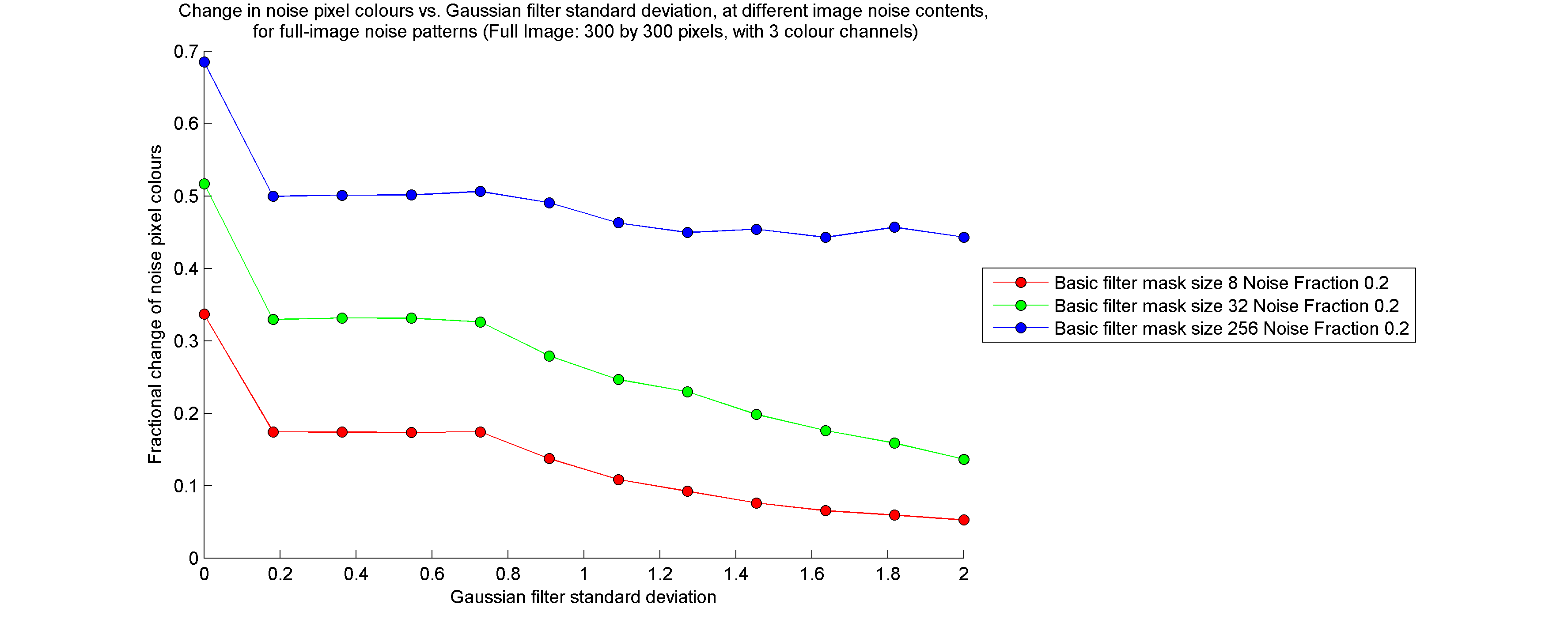
  • Noise pixel colour change: Having kept track of the positions of the initial noise pixels in the image, I am able to find the average difference (length of the average vector difference in RGB space) between noise pixel colours in the filtered image and in the original image. Next, I find the average noise pixel colour and the average background pixel colour in the original image, and then calculate the length of the difference between these two colours. The measurement of noise pixel colour change is equal to the average noise pixel colour difference divided by the length obtained in the second step.

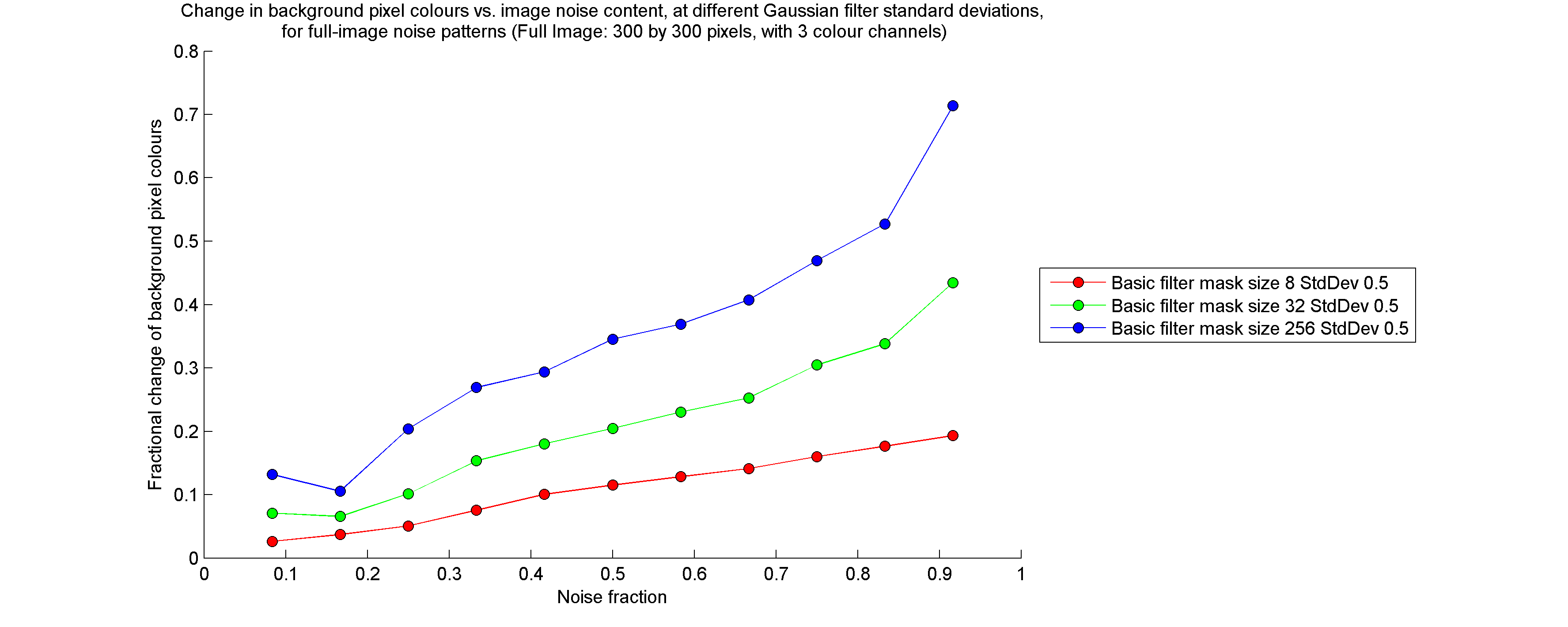
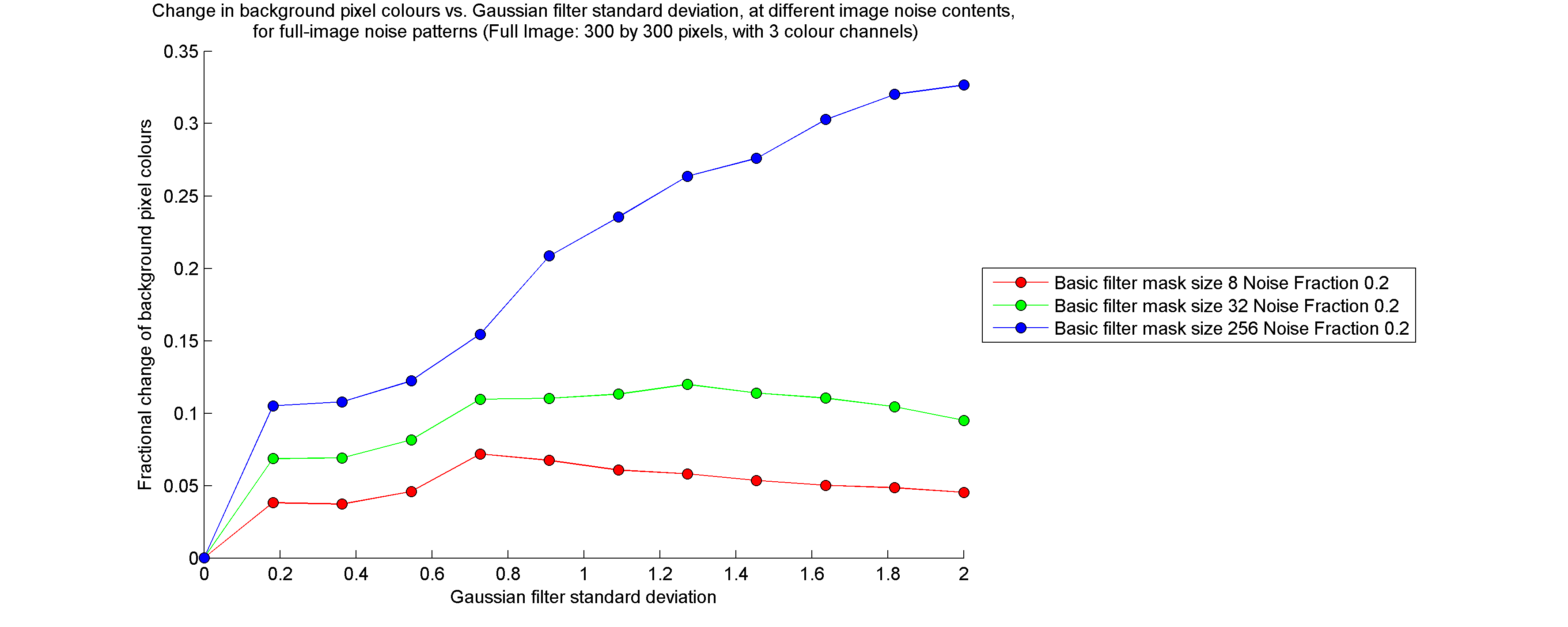
  • Background pixel colour change: This is the same as the noise pixel colour change measurement, but performed for background pixels.

Results for the Basic Cumulative Range Geodesic Filter

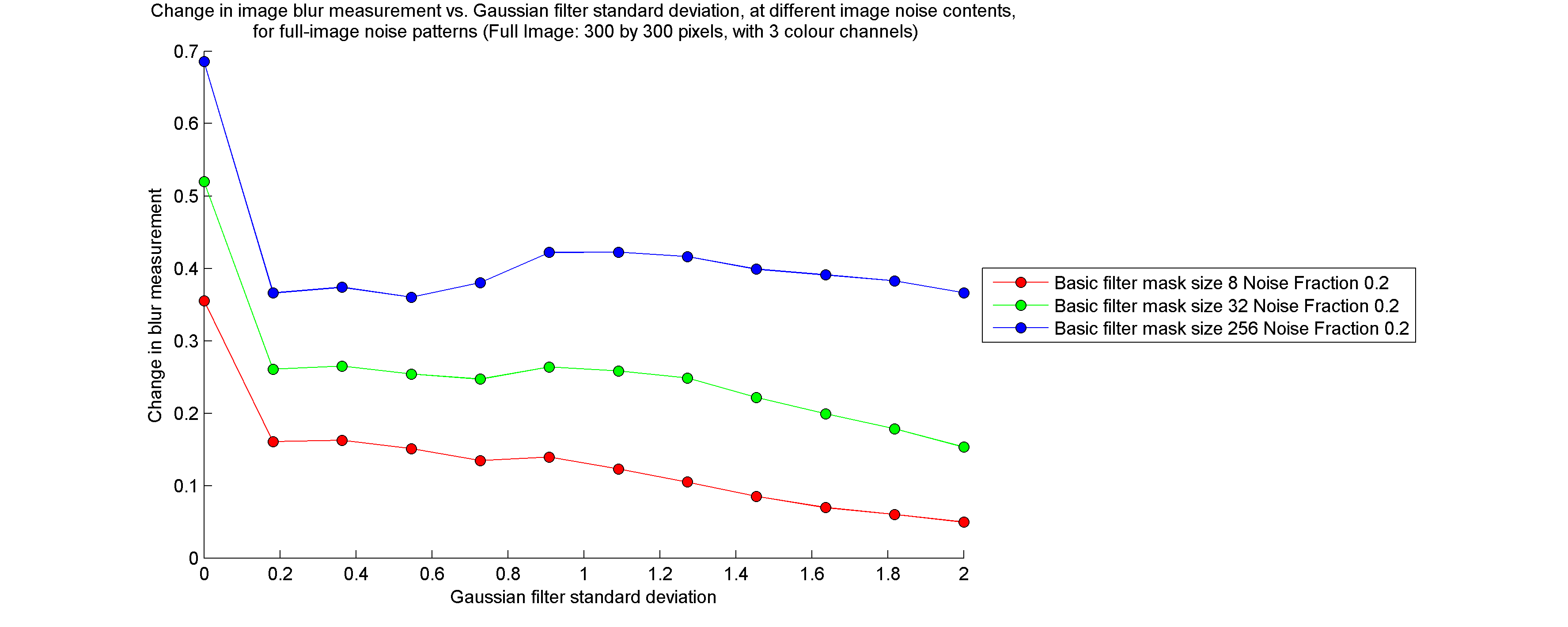
I calculated the quantities listed above for a large number of tests in which I varied filter mask size, noise pixel density (fraction of pixels which are initially assigned the noise colour), and the extent to which the noise pattern was blurred prior to being filtered. All images were filtered using a "gamma" parameter value of zero. For brevity, I have only included the results for full noise pattern images (not half noise pattern, half solid colour images) below.

Note that, while the entire image is filtered, if it is split into a solid-coloured half and a noise pattern half, the measurements described above are calculated only on the noise pattern half. Furthermore, the "noise fraction" of the image refers to the fraction of noise pixels in the noise pattern half.