Graphics, Imaging, and Games Lab

Previous Work

Dr. Mould has previously examined procedures for controlling filtering mask expansion when the mask size is not constant throughout the image. The results are contained in his article on cumulative range geodesic filtering, available at http://gigl.scs.carleton.ca/node/481

In summary, Dr. Mould found that the following method applied the appropriate amount of smoothing depending on the degree to which a pixel was an outlier or part of an outlier region in the image:

• The image was processed at a small initial mask size, say 'n', to determine the average distance from each pixel to the n^th pixels in the corresponding filtering masks, 'd_av'.
• For each pixel, a final mask size was calculated using the distance of the n^th pixel in its mask, d_n:
  • The quantity r = d_n / (f*d_av) was determined.
  • If 'r' was greater than or equal to 1, the pixel was considered an outlier, and the mask size was equal to n*(1 + r).
  • If 'r' was less than 1, the new mask size was set to 1.5*n.
  • Mask sizes were capped at a given maximum value

The effect of this method was to apply more smoothing to outlier areas and less smoothing to relatively flat areas, in order to produce an image with an equal amount of texture in all places.

Another method, developed earlier by Dr. Mould, in which mask expansion was stopped at a threshold value of cumulative distance, had the opposite effect: oversmoothing of flat regions and undersmoothing of outliers.

Objective

I would like to try controlling mask expansion during filtering, but with the intention of solving a somewhat different problem. Currently, I have not found a method I think would be more effective at producing an image with a uniform level of detail (texture) than the approach previously used by Dr. Mould. Instead, I plan to resolve the extreme fading of small contrasting features into the background colour of an image. This is actually similar to trying to preserve outliers, but I will prevent undesirable outlier preservation by introducing a parameter for a minimum mask size.

The objectives of adaptive mask termination are as follows:

• Set a mask size greater than or equal to the minimum permitted mask size, in order to smooth features below this size into their surroundings.
• Set a mask size less than or equal to the maximum permitted mask size, in order to prevent smoothing regions with little texture beyond a desired extent.
• For pixels within regions of a different colour from the background, with sizes between the minimum and maximum mask size, generate masks that are as large as possible without including pixels from the background.

Overall, this should allow for "region-aware smoothing" of the image.

Looking at Mask Pixel Distances

The central challenge which must be overcome to meet the goals listed above is detecting when the filtering mask grows into the background. As the background is a different colour from the source pixel, it makes sense to use the distances of mask pixels to answer this question, since they are derived from colour differences.

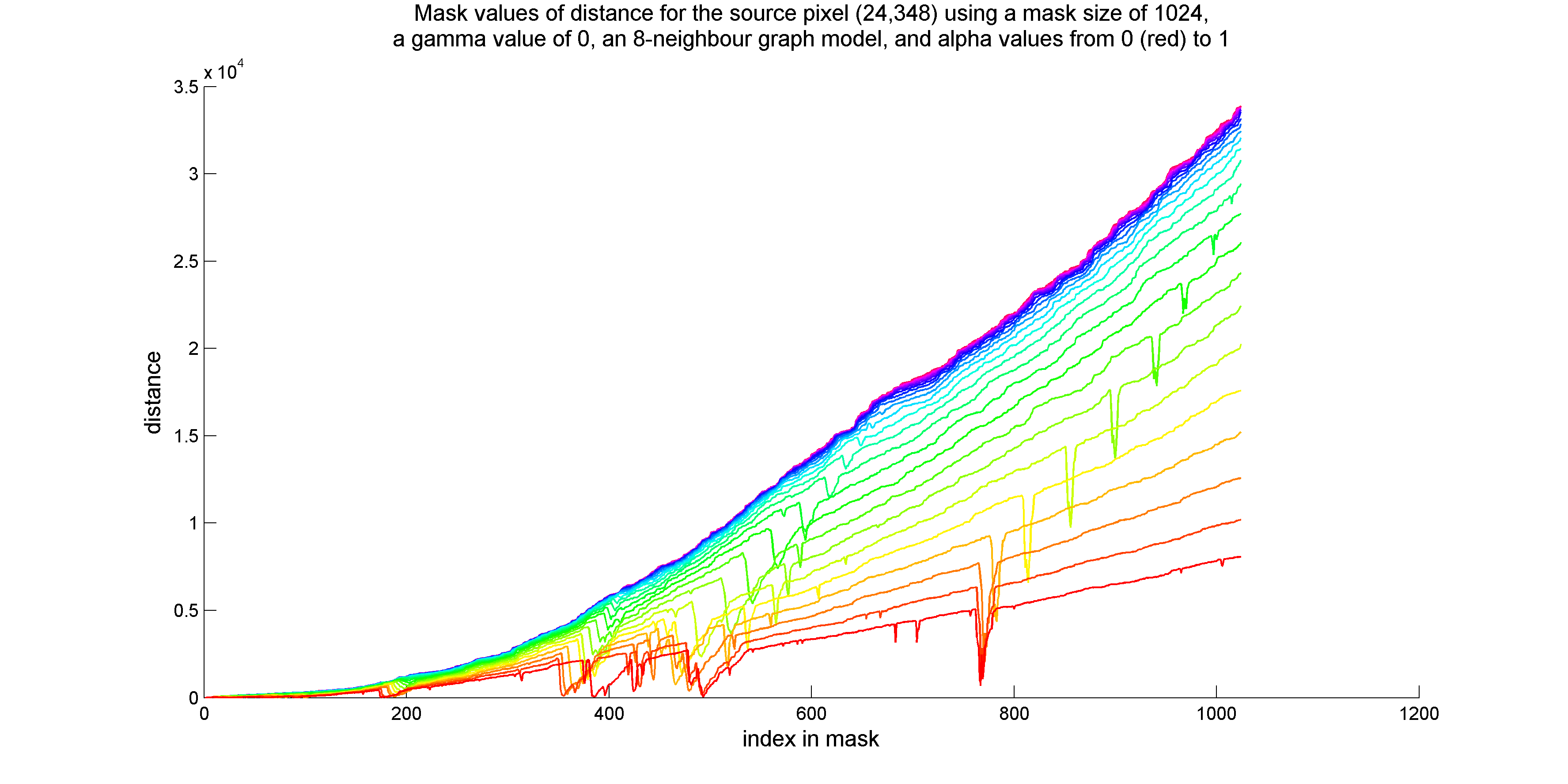
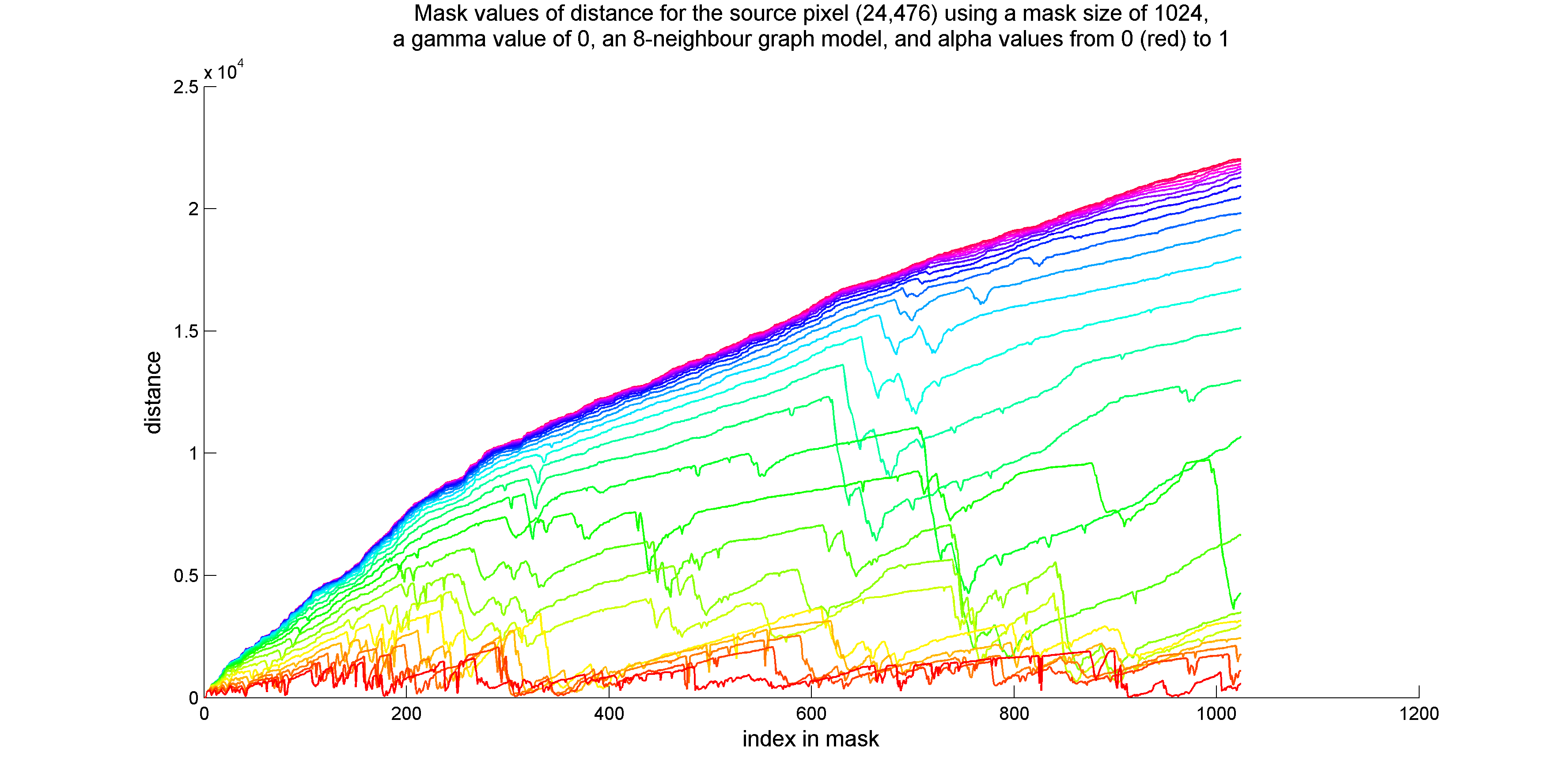
Consider the following two plots of the distance values of mask pixels as a function of their order of insertion into the mask:

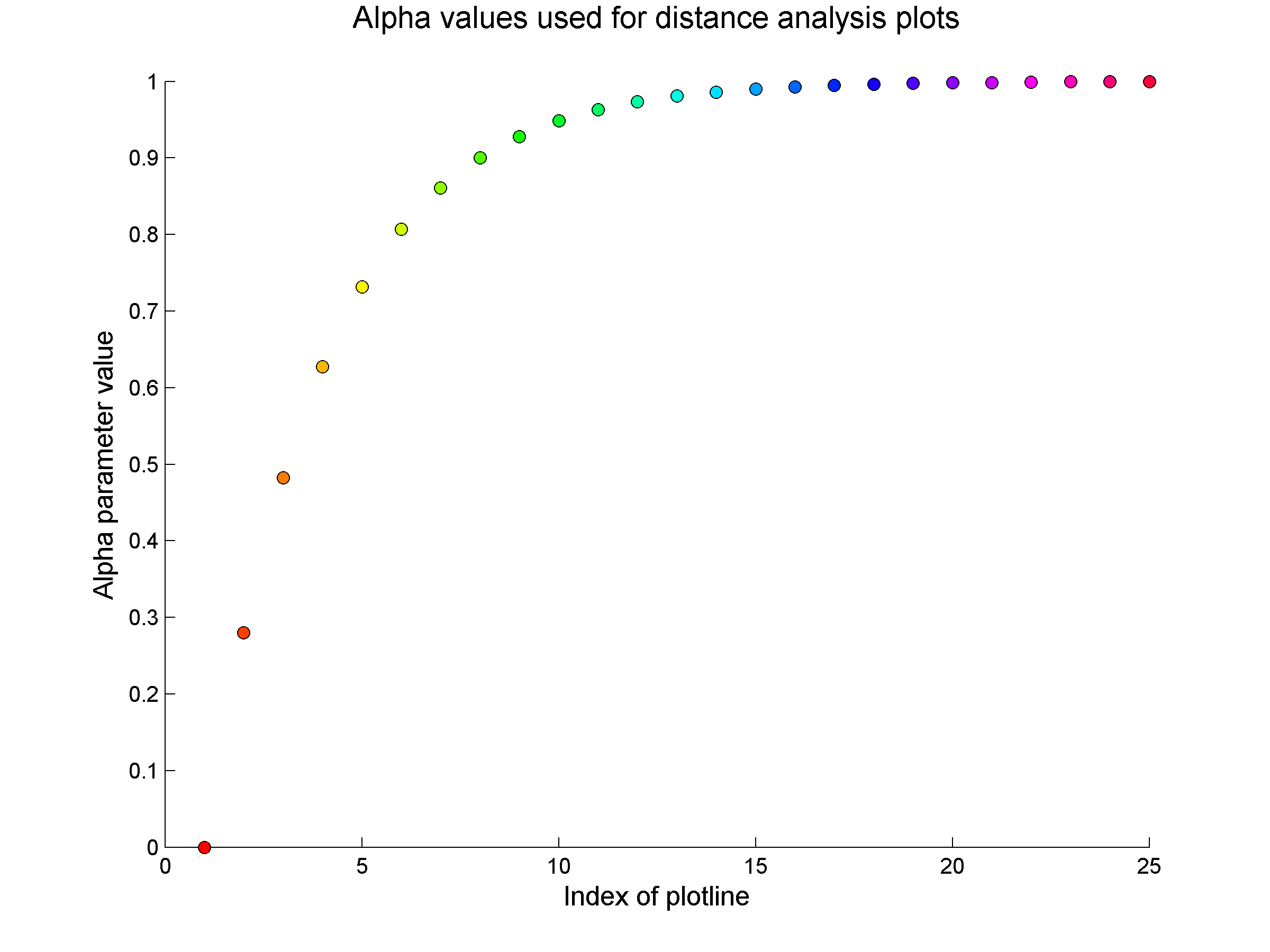
In the above plots, the value of the "alpha" parameter is increasing as shown in the following graph:

Discussion

The first plot of distances was generated for a source pixel which was part of a smooth colour gradient, while the second plot was generated for a source pixel which was located in a highly textured region.

At high alpha values, the distance curves for the two pixels have distinct shapes, so they could at least be used to estimate the relative amounts of texture in the regions surrounding each source pixel. However, because distance is a function of both colour differences and path length, it is impossible to use the curve, or the derivative of the curve, to identify where the filtering mask might have crossed into the background.

In contrast, at low alpha values, distance is mainly a function of colour difference, so the order in which pixels on the border of the mask are added to the mask depends mostly on the comparison of their colours with the colour of the source pixel. Therefore, the point at which the mask includes pixels which are part of the background is easily identified from the curve.

To achieve adaptive mask termination, I plan to stop mask growth at the point where a new pixel is added to the mask with a distance value that exceeds a given fraction of the maximum distance encountered in a mask of size equal to the maximum permitted mask size. At high values of alpha, this policy may be more or less equivalent to filtering all pixels with a constant, smaller mask size. However, at low values of alpha, the point at which the threshold distance is crossed will correlate less strongly with the number of pixels currently in the mask. In other words, the point of mask termination should be more sensitive to the characteristics of the source pixel and its surroundings.

Other data derived from distances

I considered using values of distance/(index in mask) or distance*(index in mask) for adaptive mask termination. Plots of these quantities for the two source pixels are provided below:

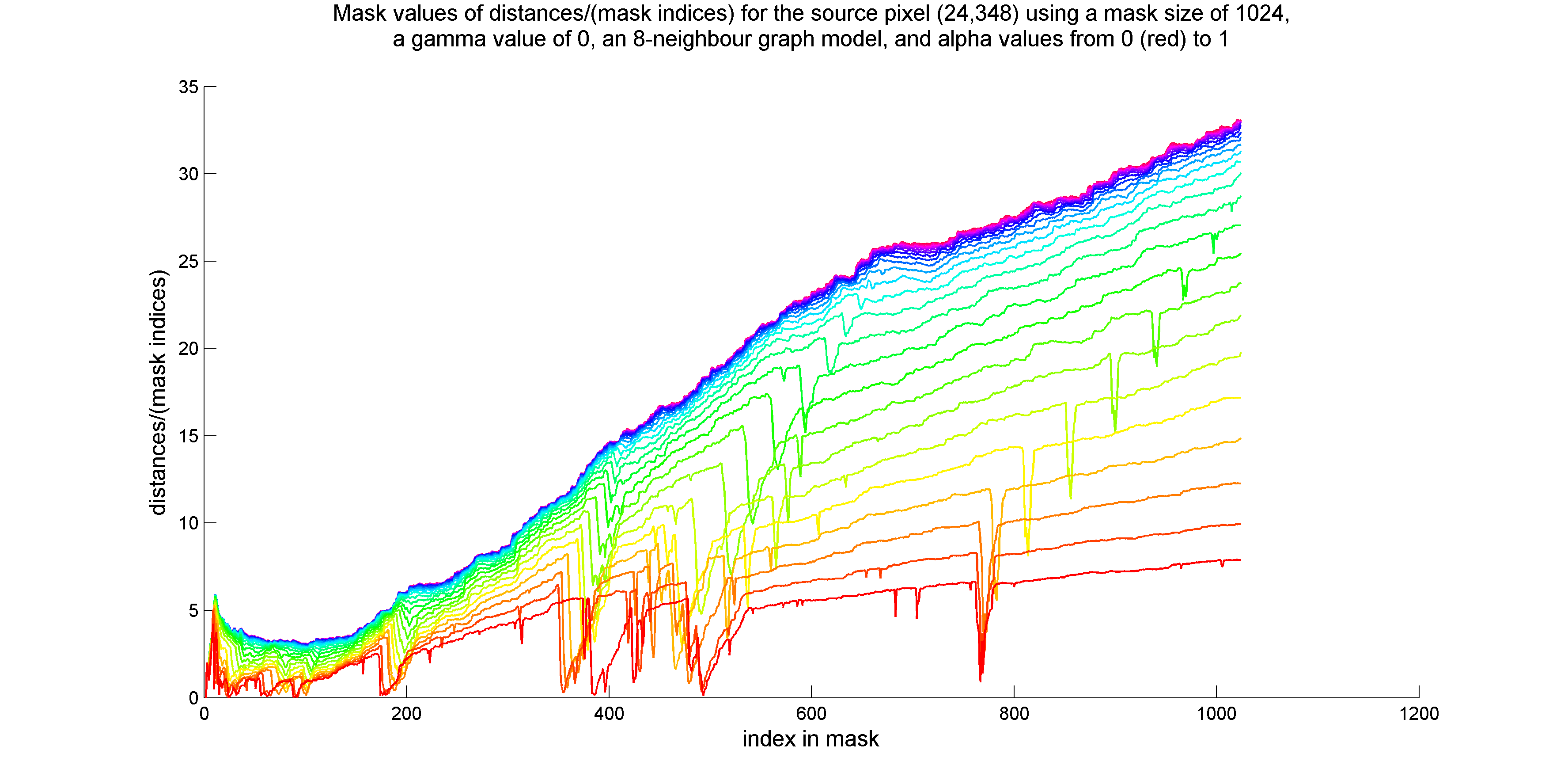
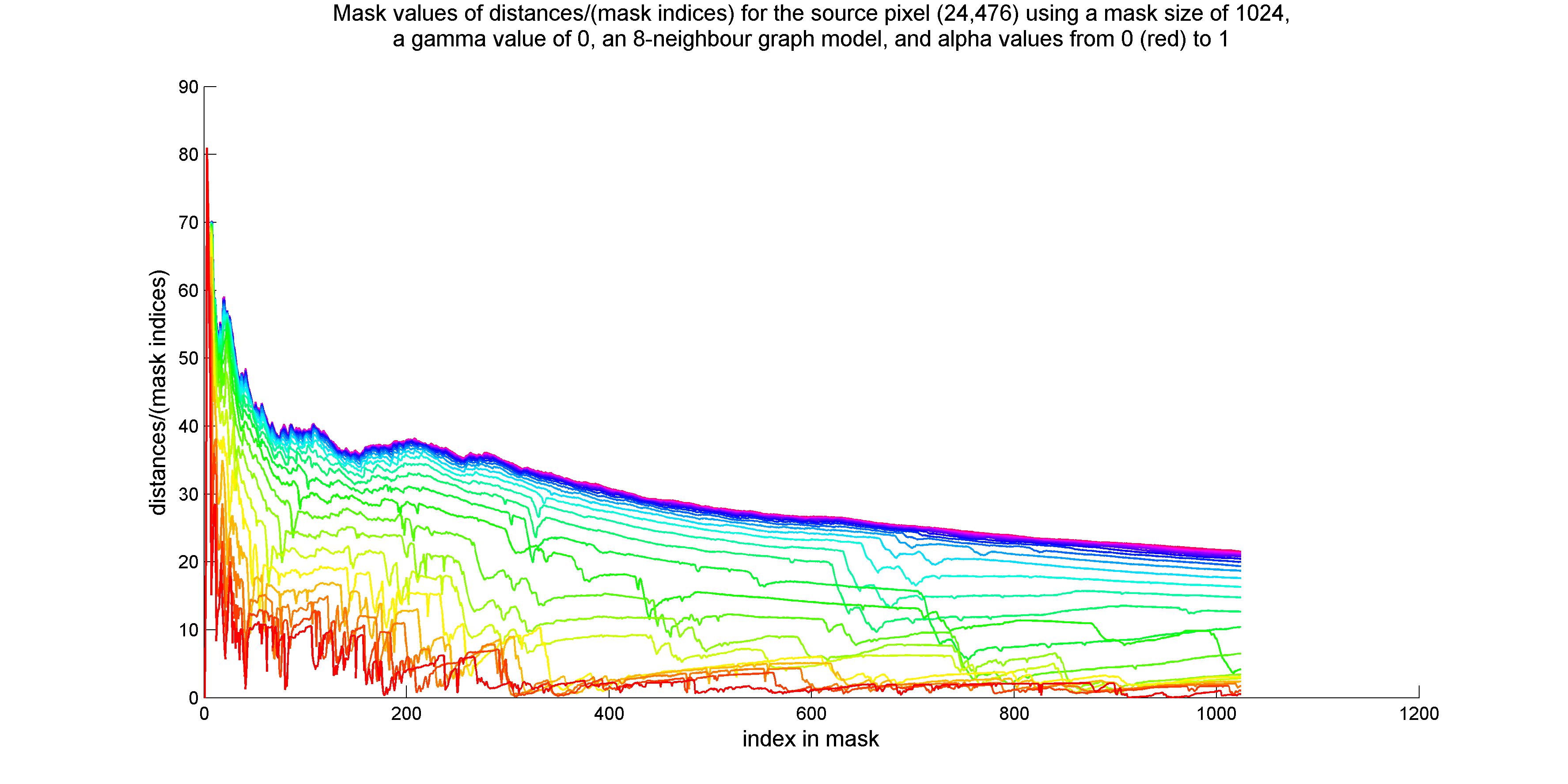
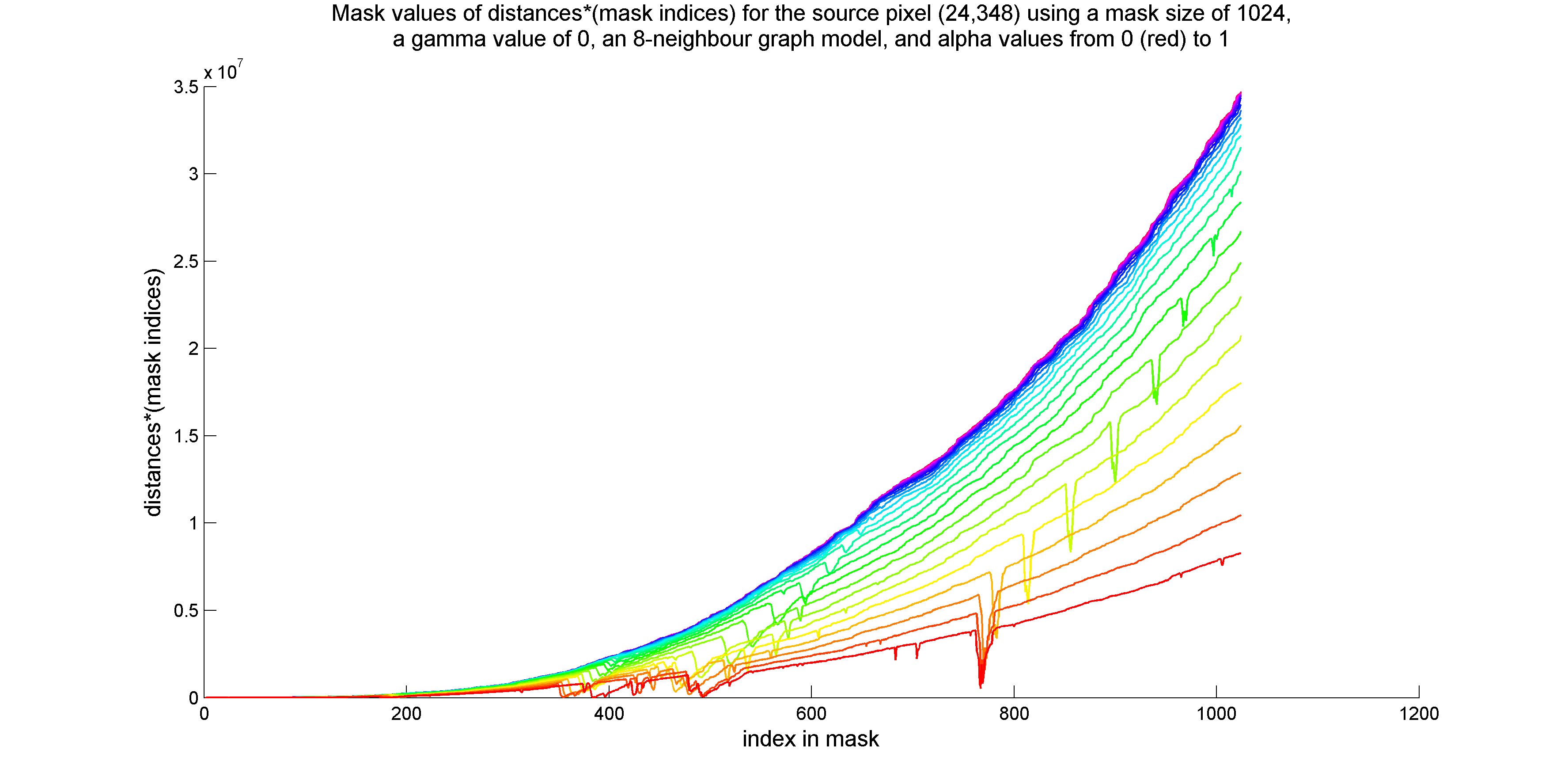
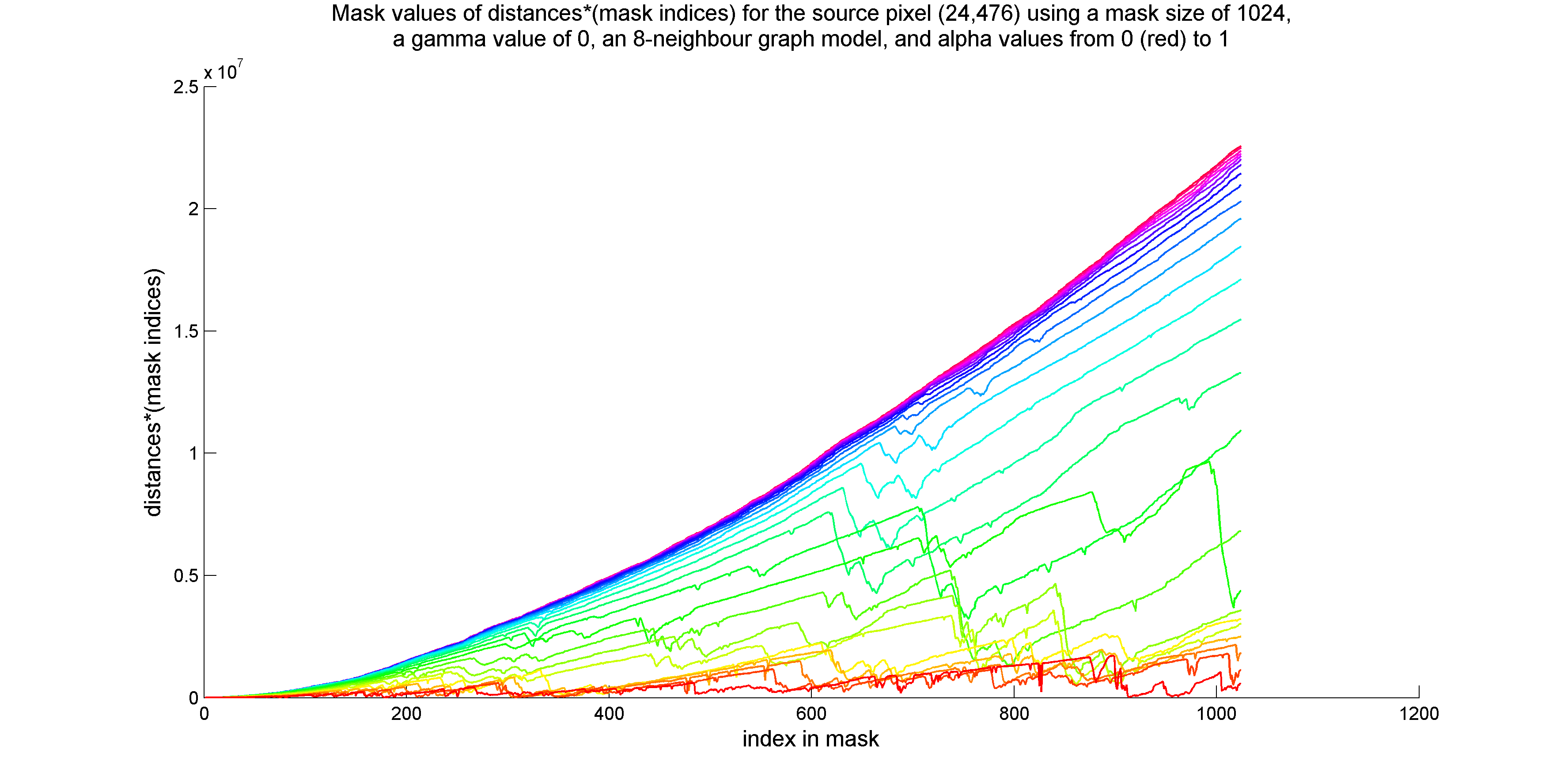
I performed a few experiments in which I terminated mask expansion at the minimum value of (distance)/(mask index), where distances were constrained to be greater than or equal to one. This method is successful at identifying the boundaries of regions similar to the source pixel. Unfortunately, if the mask passes through multiple regions that are similar to the source pixel, separated by expanses of the background colour, the end of the last region crossed became the stopping point of the mask.

So far, have not found a use for the measurement of (distance)*(index in mask).