1. Problem

As shown in the figure 1, assume there are two particles A and B moving parallel, the distance between A and B is known, and d(AC) = d(CB). Now we add a new particle V starting from A's position, moving towards the middle line of AB. Point R shows the x-coordinate of V.

This post aims the problem of defining V's movement so that the path of it will shape a smooth tangent-like curve as shown in figure 1.

        (figure 1)

2. Solution

1) Get corresponding tangent value of particle's location

First, we need to transform particle's coordinate so that we could use it in tangent function.

We know that:

Distance of A and R: d(AR)     (NOTE: In practice, since A and B move together with point V, so it should be fine to use d(AV) directly)

Distance of A and C: d(AC)

Let a float type ratio = d(AR) / d(AC). Since the path in figure 1 is one cycle in tangent function from -PI/2 to PI/2 (see figure 2 red curve), if we define X(x,y) as a corresponding point of V on tangent's graph, then: 

ratio = d(A'x) / d(A'C')   (NOTE: A' = -PI/2 and C' = PI/2, x here is the value of x-coordinate)

         = d(A'x) / PI

For each position of V on path p, we could find the corresponding tangent value as tan(x). For example:

d(A'x) = PI * ratio;

x = d(A'x) - A = PI * ratio - PI/2; 

then the corresponding tangent value of V at that time could be obtained from tan(PI * ratio - PI/2)

 (figure 2)

2) Get slope value

Apparently, the tangent line of the red curve in figure 2 gives the direction of particle V at each moment. We know that: slope value = tangent of the angle of the slope, so we need to get the slope value of tan(x) by taking derivative:

slope = d/dx * tan(x) = sec(x) * sec (x)

As shown in figure 2, the blue dash line indicates the derivative of tan(x), point S in y-coordinate is the corresponding slope value of X. 

The angle of the slope could be obtained:

angle = arctan(slope).

3) Get direction

By now, we got the angle of the slope of path p, aka, the angle of V's direction.

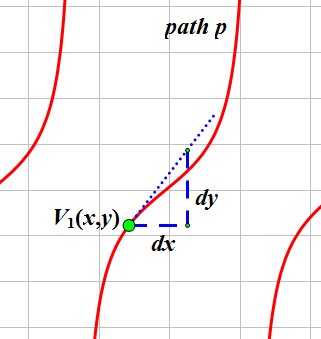   (figure 3)

In figure 3, V1 locates at (x,y), the blue tangent line points the current direction. For each unit value dx, we could get the dy by tan(angle). So the direction of V1 could be obtained as:

dir.x = 1;

dir.y = tan(angle);

dir.normalize();         (NOTE: since tan(angle) = slope, we could also skip the step calculating angle and simply use slope)

Now we get the general method to calculate a particle's direction moving along a tangent-like path.

At anytime, simply use:

pos.x += v * dir.x;

pos.y += v * dir.y;      (NOTE: vector "pos" denotes the current postion of a particle, scalar "v" represents the speed)

to update the particle's position.