1. By changing the spacing threshold for lines, our coordinated particle system can provide different effects while the behavior of particles still stays the same. Here are some results that we tested (note that some of the images below need to be zoomed in to observe):

Take an input image, we use one particle group release particles inside of foreground objects, while another group take care of the background. The two particle groups will not interrupt with each other, and each particle only performs coordinated movement with members inside a same group.

Check the previous blog post for more information: Spacing Control for Coordinated Particle System (1)

We have managed changing the spacing for each pair of particles, now we try to make it change slowly and smoothly.

Instead of making each pair of particles adjust to the new spacing immediately when particles enter a new area with different spacing, we give these particles an "adjusting" time.

Each particle will remember the old spacing that they were on. When particle A enters a new area with spacing 30 from the old area which has a spacing as 10, it will first compare its own old record with the current spacing, if the record is smaller, make it somewhat larger, and vice versa. In this case, A's old record will be added by 0.001. When it comes to compare the distance of A and its neighbor B with the spacing, to determine if there is a need of birth or death, it will compare the distance AB with the average of A and B's records. 

In this case, if AB > BIRTH_OFFSET * (A_record + B_record) / 2, then generates a new particle between A and B; if AB < DEATH_OFFSET * (A_record + B_record) / 2, then kill B;

By this way, AB will not just compare with the new current spacing, so that when the old spacing and the new one are too different, particles will not have a burst of birth or death suddently .

See the images below showing the effect of this feature.

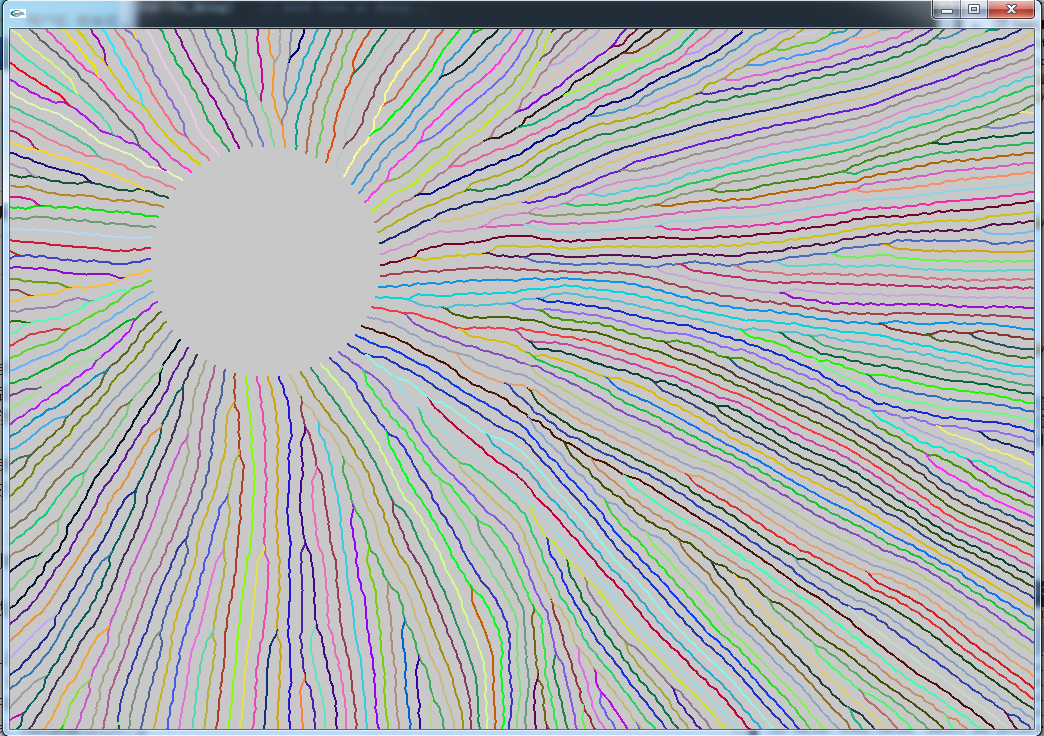
If we have an attribute of spacing value for each pixle in a map, and particles will have to follow the spacing value to adjust their distance with neighbors, we then can control the spacing of particles based on an image. And if the spacing value is associated with the gradient value, the particles will be able to shape object in the image by changing their spacing.

As shown in the image below, there are two parts of spacing area on the canvas. When particles enter an area with a smaller spacing, the less chances they would kill adjacent neighbors and more possibilities to generate a new one.

The codes of space control (AB is the distance between particle A and B; Td is the threshold of current pixel; and V is a spacing viable for the current pixel):

average_Td = A_Td + B_Td;         // get the average threshold of pixels that A and B currently in

average_V = A_V + B_V;               // get the average viable

BTH_offset = 1.41;

DTH_offset = 0.58;

if (AB<DTH_offset * average_Td * average_V)

merge A and B as one particle;

else if (AB>BTH_offset * average_Td * average_V )

create a new particle between A and B;

//NOTE*: All the pixels on the left half of the canvas is set as: V = 1; and the right half is: V = 0.8. The threshold Td is set as 10 through out the canvas.

One of the features of ths project is to let all particles grow themselves yet not crossing with each other.  Each particle is stored in array, and knows the distances with two adjecent neighbors. When two neighboring particles grow too close to each other, one of them will be killed to avoid collision. However, when two particles which are not neighbors about to cross, they cannot simply be alerted using this method.

We try to solve this with the idea below:

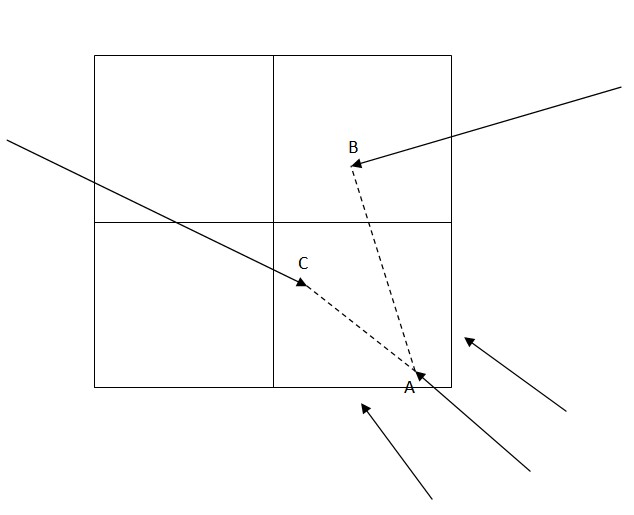
1. Divide the whole screen into grid cells, the size of the grid cells can be changed as need. Each particle will remember the grid ID that it is currently in and register in that grid. If the total number of particles that have registered in the grid cell exceeds a threshold, the grid then is blocked and no new particles could enter. When a particle enters a new grid cell, it will: a) Check if this grid cell is still available. b) If the grid is still vacancy, update its current grid ID and register in the grid.
2. There are two cases of collision: collide with particles which are also currently inside the grid; collide with the traces which are left by particles before.
3. The possible solution to prevent the cases is:  Get the information of other registered particles, check the distance with them, kill if needed; When there is a particle enter and leave without collisions, or two particles died, the grid cell is then marked as blocked, no more future particles can enter.

For example: As shown in figure below, when particle A enters this grid, it gets the information of B and C, thereby keeping checking the distance between each other. A, B and C can be killed all together when there is a death need.

1. Problem

As shown in the figure 1, assume there are two particles A and B moving parallel, the distance between A and B is known, and d(AC) = d(CB). Now we add a new particle V starting from A's position, moving towards the middle line of AB. Point R shows the x-coordinate of V.

This post aims the problem of defining V's movement so that the path of it will shape a smooth tangent-like curve as shown in figure 1.

        (figure 1)

2. Solution

1) Get corresponding tangent value of particle's location

First, we need to transform particle's coordinate so that we could use it in tangent function.

We know that:

Distance of A and R: d(AR)     (NOTE: In practice, since A and B move together with point V, so it should be fine to use d(AV) directly)

Distance of A and C: d(AC)

Let a float type ratio = d(AR) / d(AC). Since the path in figure 1 is one cycle in tangent function from -PI/2 to PI/2 (see figure 2 red curve), if we define X(x,y) as a corresponding point of V on tangent's graph, then: 

ratio = d(A'x) / d(A'C')   (NOTE: A' = -PI/2 and C' = PI/2, x here is the value of x-coordinate)

         = d(A'x) / PI

For each position of V on path p, we could find the corresponding tangent value as tan(x). For example:

d(A'x) = PI * ratio;

x = d(A'x) - A = PI * ratio - PI/2; 

then the corresponding tangent value of V at that time could be obtained from tan(PI * ratio - PI/2)

 (figure 2)

2) Get slope value

Apparently, the tangent line of the red curve in figure 2 gives the direction of particle V at each moment. We know that: slope value = tangent of the angle of the slope, so we need to get the slope value of tan(x) by taking derivative:

slope = d/dx * tan(x) = sec(x) * sec (x)

As shown in figure 2, the blue dash line indicates the derivative of tan(x), point S in y-coordinate is the corresponding slope value of X. 

The angle of the slope could be obtained:

angle = arctan(slope).

3) Get direction

By now, we got the angle of the slope of path p, aka, the angle of V's direction.

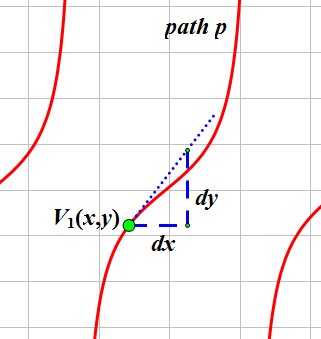   (figure 3)

In figure 3, V1 locates at (x,y), the blue tangent line points the current direction. For each unit value dx, we could get the dy by tan(angle). So the direction of V1 could be obtained as:

dir.x = 1;

dir.y = tan(angle);

dir.normalize();         (NOTE: since tan(angle) = slope, we could also skip the step calculating angle and simply use slope)

Now we get the general method to calculate a particle's direction moving along a tangent-like path.

At anytime, simply use:

pos.x += v * dir.x;

pos.y += v * dir.y;      (NOTE: vector "pos" denotes the current postion of a particle, scalar "v" represents the speed)

to update the particle's position.