Graphics, Imaging, and Games Lab

I decided to start exploring how to filter out noise pixels from an image by implementing an idea that Dr. Mould had brought up with earlier. Dr. Mould suggested that outliers could potentially be identified by the number of times that they are added to filtering masks for the surrounding pixels, relative to other pixels in the image. In order to use this measurement, I created a two-pass filter, in which the entire image is first processed at a given mask size and the number of times that each pixel is included in a filtering mask is recorded. Next, the image is filtered in a way which makes use of the data obtained during the first pass, using the same or a different mask size.

Methods

For simplicity, I removed the "gamma" parameter from the filtering algorithm before developing the two variations described below. In other words, the incremental cost of adding a pixel to a filtering mask is given only by the colour difference between the pixel in question and the source pixel of the mask (as though "gamma" is zero).

Distance Weighting Method

In this version of the filter, I use the array storing the number of times that each pixel was part of a first-pass filtering mask to control the mask generation process during the second pass. Specifically, the incremental distance of each pixel is divided by its count of mask inclusions, before being added to the distance to the previous pixel along the path. As a result, pixels which were part of more filtering masks during the first pass will be preferentially selected to be part of second-pass filtering masks.

Average Weighting Method

A second version of the filter uses the array storing the number of times that each pixel was part of a first-pass filtering mask to weight pixels when determining the output image. Specifically, each pixel in a given filtering mask is multiplied by its count of mask inclusions before being added to the colour sum for the current source pixel. Consequently, this version of the filter generates the same filtering masks on both passes, but the colour of each pixel in the filtered image is more strongly determined by the pixels in its mask that were present in a larger number of masks overall.

Filtering Results

Note that, in all figures below, the "normal filter" refers to the published version (described here), with a "gamma" parameter value of zero. The normal filter is a single-pass filter. In the figures below, "second-pass mask size" refers to both the single mask size value of the normal filter and the second-pass mask sizes of the two-pass filters.

Source Image

Filtering at a constant first-pass mask size of 128, at varying second-pass mask sizes

Filtering at a constant second-pass mask size of 512, at varying first-pass mask sizes

(All three images for the normal filter are identical.)

It appears, from the two sets of images shown above, that there is very little difference between any of the filters. The average weighting method produces slightly smoother images than the distance weighting method. Both of the two-pass filters produce slighlty smoother images than the single-pass filter.

Perhaps the most observable effect of the two-pass filters seen in the images above is the fading of the nostril towards the colour of the nose, especially at higher first-pass mask sizes.

Changing first-pass mask size has relatively little effect on the output image compared to changing the second-pass mask size. In particular, changing the first-pass mask size at low second-pass mask sizes results in a negligible change to the image. In general, the two-pass filters seem to follow the same trends that I reported at http://gigl.scs.carleton.ca/node/522 for plane-fitting filters:

• Applying a special technique to the averaging process seems to have a greater effect on the filtered image than applying it to the mask building process.
• Different variations of the cumulative range geodesic filter can yield remarkably similar results.

With respect to image smoothing, my favourite filter so far is the plane-fitting filter which used fitted planes to replace the colour averaging process (see http://gigl.scs.carleton.ca/node/522) .

Comparison of "Behind the Scenes" Behaviour

I am a bit disappointed by the seeming lack of change in the output of the two-pass filters relative to the normal single-pass filter. On the other hand, I find the visualization of the number of times that each pixel was added to a first-pass filtering mask quite interesting. Perhaps this process can be used for texturing or recolouring an image.

Counts of first-pass mask inclusions

In the above image, brighter values mean that the pixel was added to more first-pass masks. All images have been scaled to greyscale colours in the full range of 0-255. As a result, the shades of grey span a larger set of counts in the right-hand frames of the montage.

Notice that the nostril, for instance, was not frequently included in first-pass masks, which corresponds to its fading in the filtered images shown earlier. This relationship is easily seen in the montage below, which shows the weights assigned to selected pixels by the weighted averaging two-pass filter.

Visualization of pixel weights during averaging by the average-weighting two-pass filter

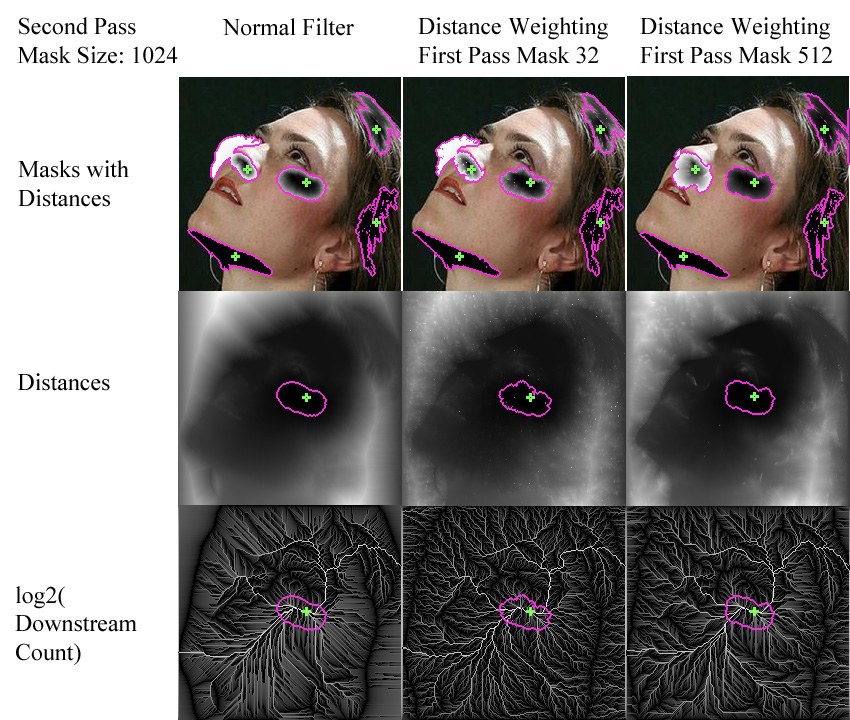
Despite the similarities in the output images, a look inside the second-pass mask generation process for the distance-weighting filter shows considerable differences from the normal filter:

Second Pass Distance Values and Downstream Counts

Comparison of Noise Pattern Filtering

In order to isolate the performance of each filter with respect to noise removal, I filtered random noise patterns. Refer to http://gigl.scs.carleton.ca/node/535 for an explanation of the details of this procedure. The results, shown below, indicate that the distance-weighting filter was slightly more successful in removing noise than the normal filter, while the average-weighting filter was the most successful in removing noise out of all three filters.

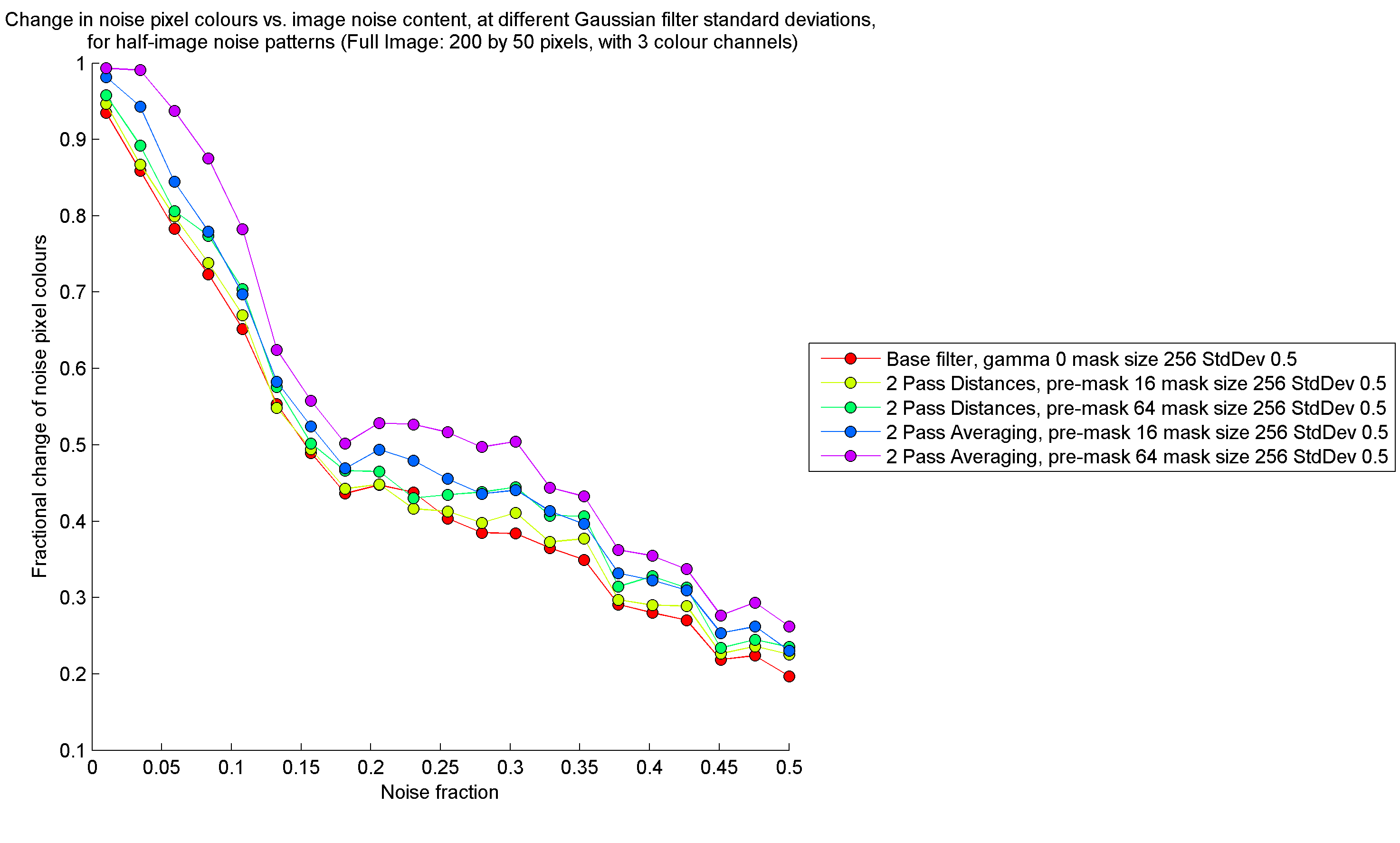
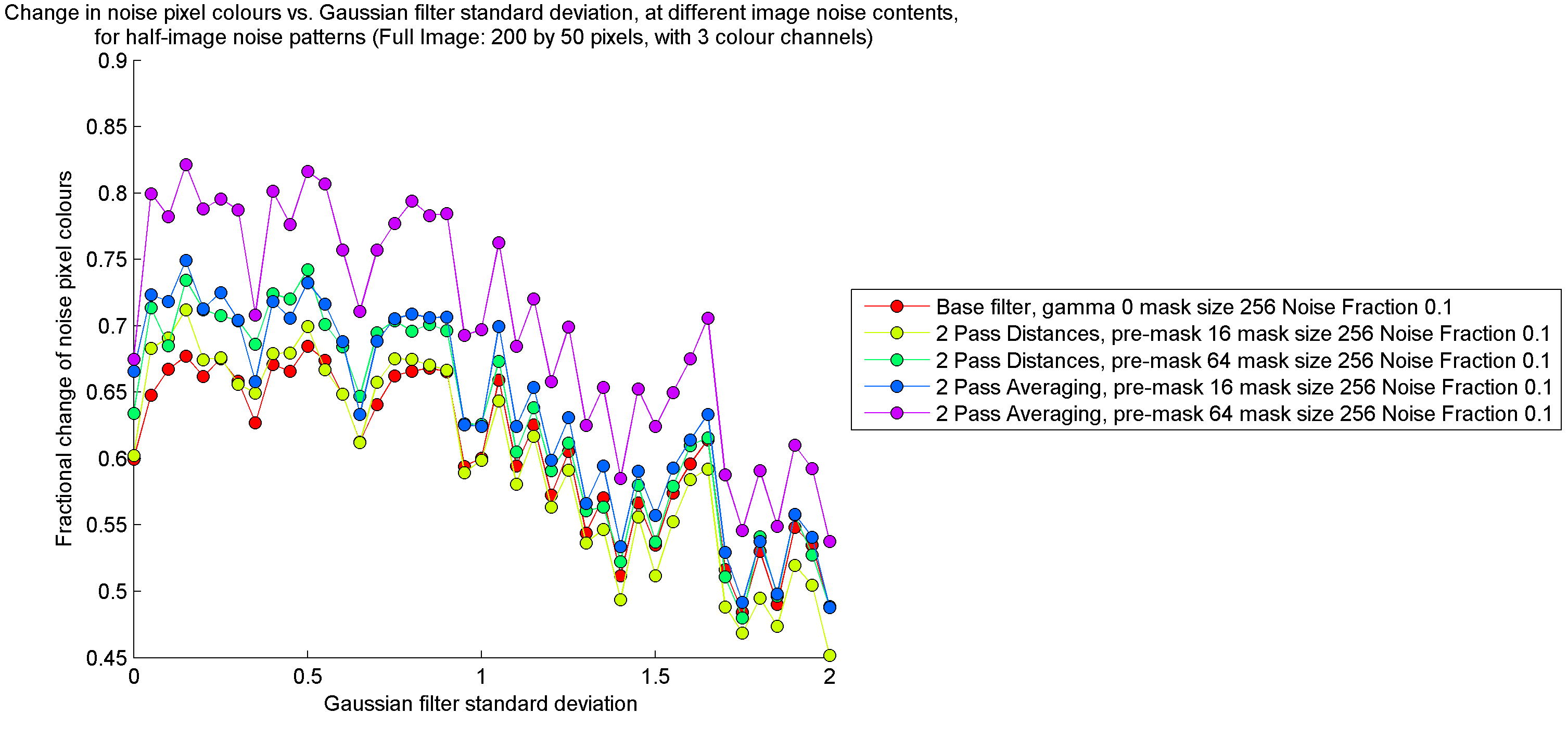
On the other hand, at high noise contents, it seems that the two-pass average-weighting filter contaminates non-noise pixel colours to a greater extent than the normal filter, while the distance-weighting filter does the reverse.

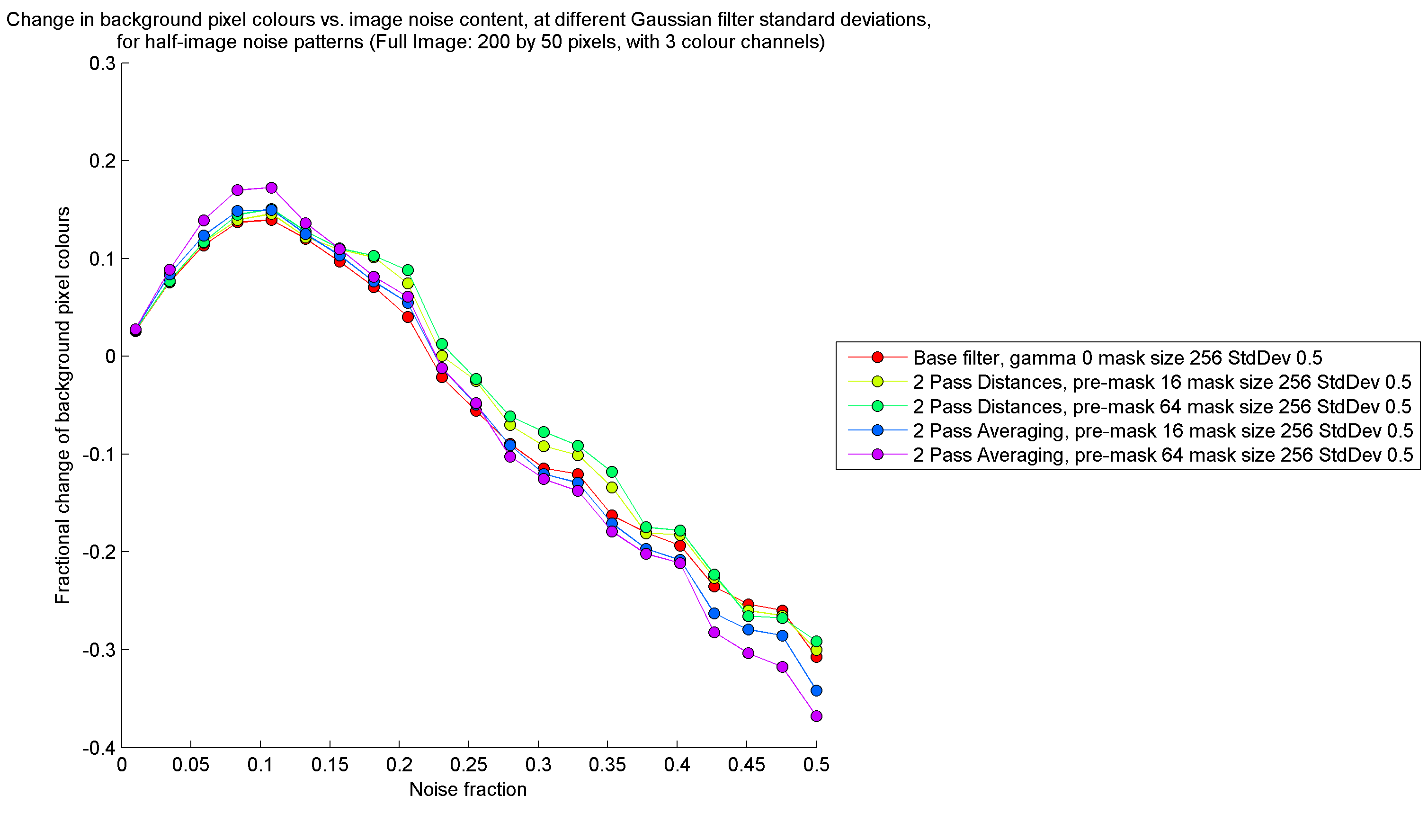
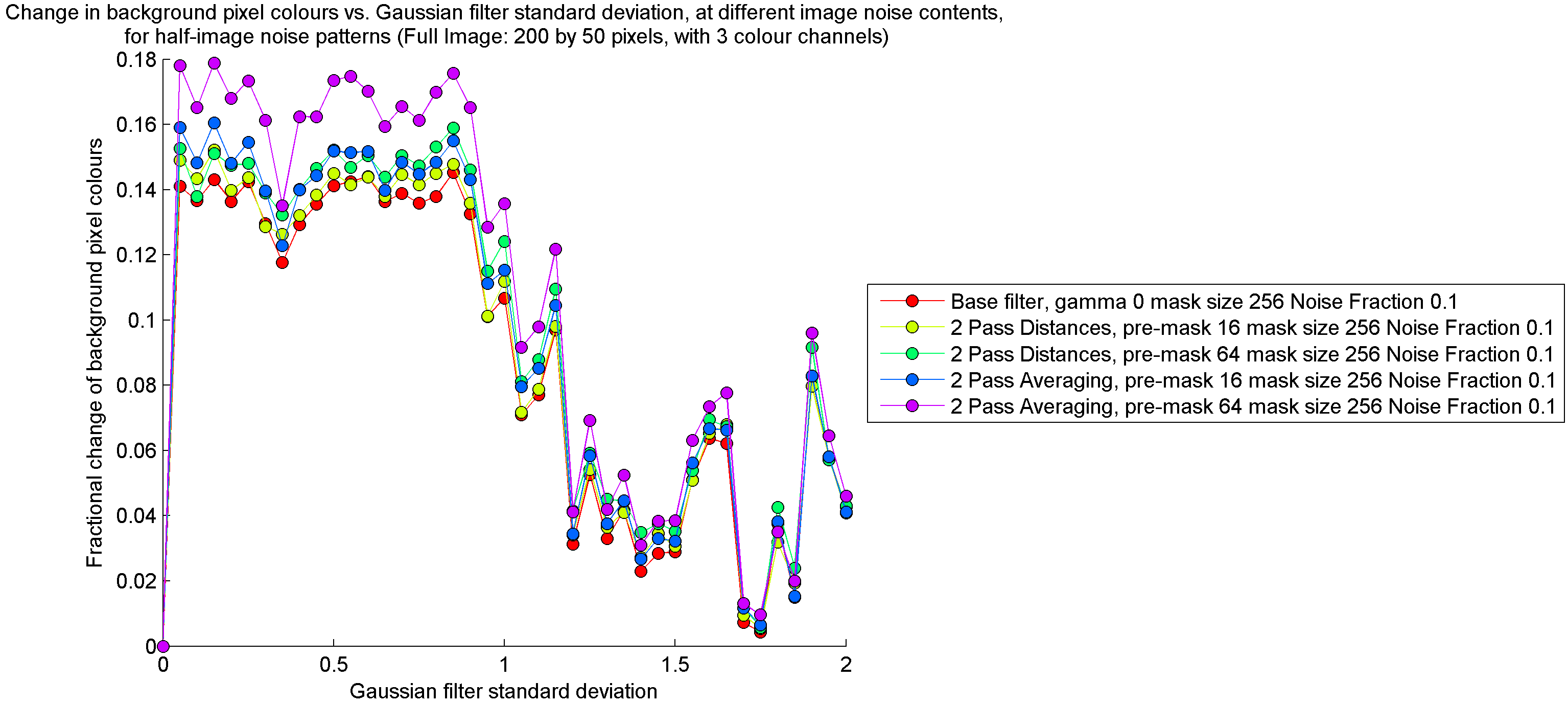
Conclusions

Overall, the two-pass filters do not represent a dramatic improvement over the normal, single-pass filter. In particular, looking at the actual noise pattern test images, it appears that the two-pass filters do not solve the problem posed by outlier pixels adjacent to regions with the same colour:

Comparison of Noise Pattern Unfiltered and Filtered Images (10 percent noise, Gaussian blurring function standard deviation of zero)

In contrast, all three filters are fairly effective at removing isolated outliers in large expanses of normal pixels, so there is less room for improvement with respect to this criteria. Therefore, it seems that the problem of outlier reduction comes mainly from the fact that outlier pixels generate masks which help to sustain them. I have most likely already developed filter variations which combat this issue: The plane-fitting filters described at http://gigl.scs.carleton.ca/node/522. To verify this, I will run the noise pattern tests on the plane-fitting filters to see how they compare with the normal filter.

Portrait image source:

Page 2 of Geodesic Image and Video Editing, by Criminisi et al. (ACM Transactions on Graphics, Vol. 29, No. 5, Article 134, Publication date: October 2010.)