Graphics, Imaging, and Games Lab

Introduction

In this post, leaky integration refers to a calculation similar to integration, except that the integrand is multiplied by an increasing exponential function. The exponential function has a value of 1 at the upper boundary of integration.

To produce the results shown in this post, I created a version of the cumulative range geodesic filter which uses leaky integration as follows: The distance to each pixel in a filtering mask is equal to the incremental distance between the current pixel and the previous pixel along the path from the source pixel, added to the leaky sum of the incremental distances between the other pixels along the path.

In the normal cumulative range geodesic filter, distances were computed as follows: D(p_N) = d(p_N) + d(p_N-1) + d(p_N-2) + ... + d(p₁) + D(p₀), where

• D(p_N) is the distance from the source to the current pixel.
• d(p_i) is the incremental distance between pixels i and i-1.
• D(p₀) is the starting distance value of the source pixel (equal to zero).

In contrast, the leaky integration version of the filter uses the following calculation for distance: D(p_N) = d(p_N)*(f⁰) + d(p_N-1)*(f¹) + d(p_N-2)*(f²) + ... + d(p₁)*(f^N-1) + D(p₀)*(f^N), where

• f is a value between 0 and 1 (including 0, but not including 1). In the rest of the post, I will refer to f as the "alpha" parameter of the filter.

Comparison with other filtering methods: Portrait image filtering

Source Image

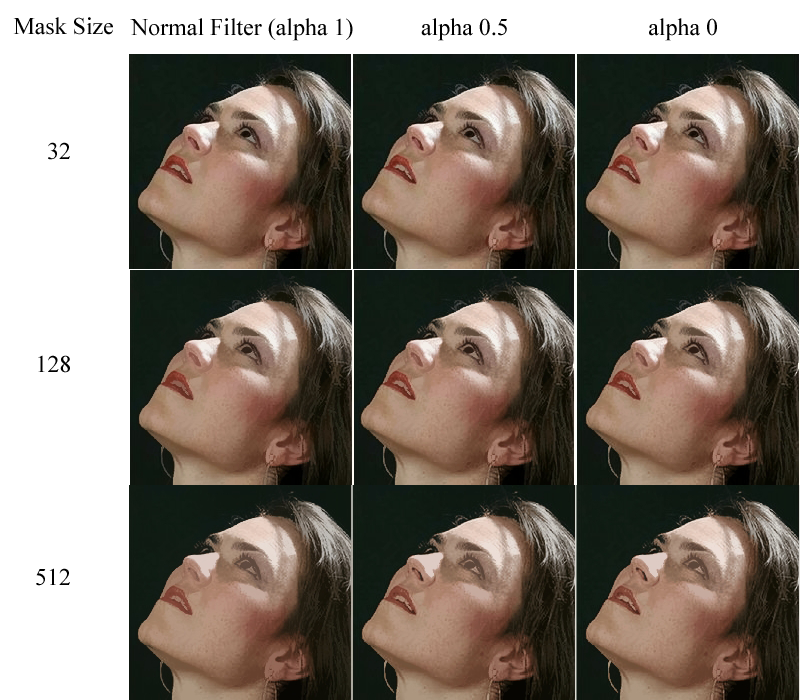
The results of filtering the image at a few different mask sizes and "alpha" values are provided below. Evidently, as the value of alpha decreases, the amount of smoothing decreases, and there is more noise in the output image. On the other hand, small features in the image, such as the nostril, are better preserved at low alpha values, assuming that they cover an area which is greater than or equal to the mask size. (If the mask size is larger than the feature size, the mask must include pixels outside the feature, causing contamination from the background colours.)

For a glimpse into the mechanisms underlying the trends shown above, examine the following montage of images, which were produced using a mask size of 1024:

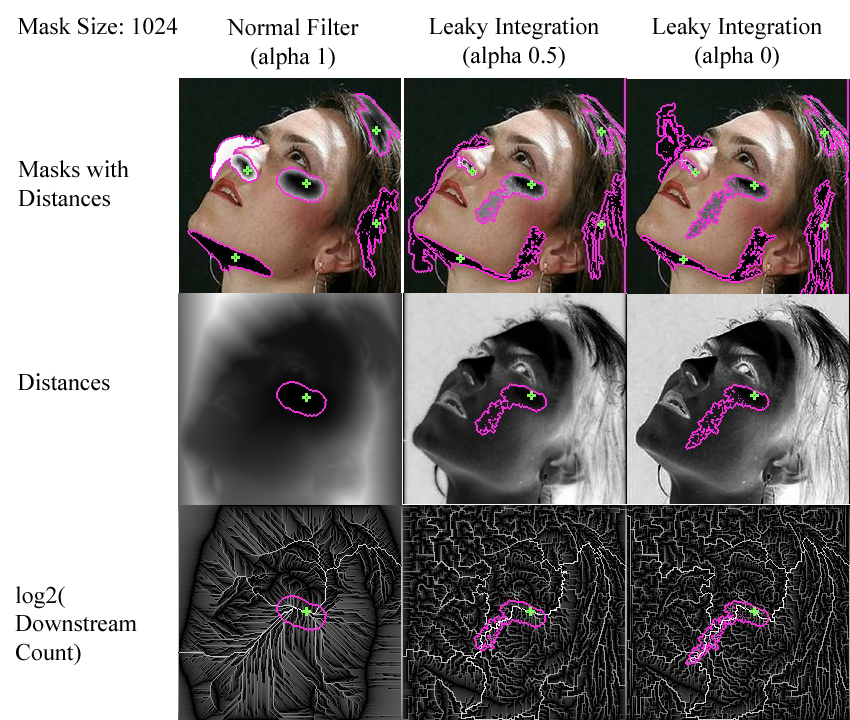
As the value of alpha decreases, filtering masks elongate since the colour difference betwen the source pixel and the current pixel is more heavily weighted than the sum of colour differences along the path leading up to the current pixel. In other words, the length of the path has a smaller effect on the cost of adding a given pixel to the mask.

I find the visualizations of downstream counts particularly interesting. The normal filter always seems to exhibit a kind of two-phase downstream plot. Near the source pixel, paths are highly convoluted. However, at a certain distance away from the source pixel, paths align and straighten into large sloping features. I hypothesize that the straightening of paths is due to the increasing importance of spatial distance over colour differences. This idea seems to be supported by the downstream plots produced at lower values of alpha, which have mostly convoluted paths. This indicates that colour differences remain important when new pixels are examined for inclusion in the mask, even as the mask becomes very large.

Portrait Image Source: Page 2 of Geodesic Image and Video Editing, by Criminisi et al. (ACM Transactions on Graphics, Vol. 29, No. 5, Article 134, Publication date: October 2010.)

Comparison with other filtering methods: Noise pattern filtering

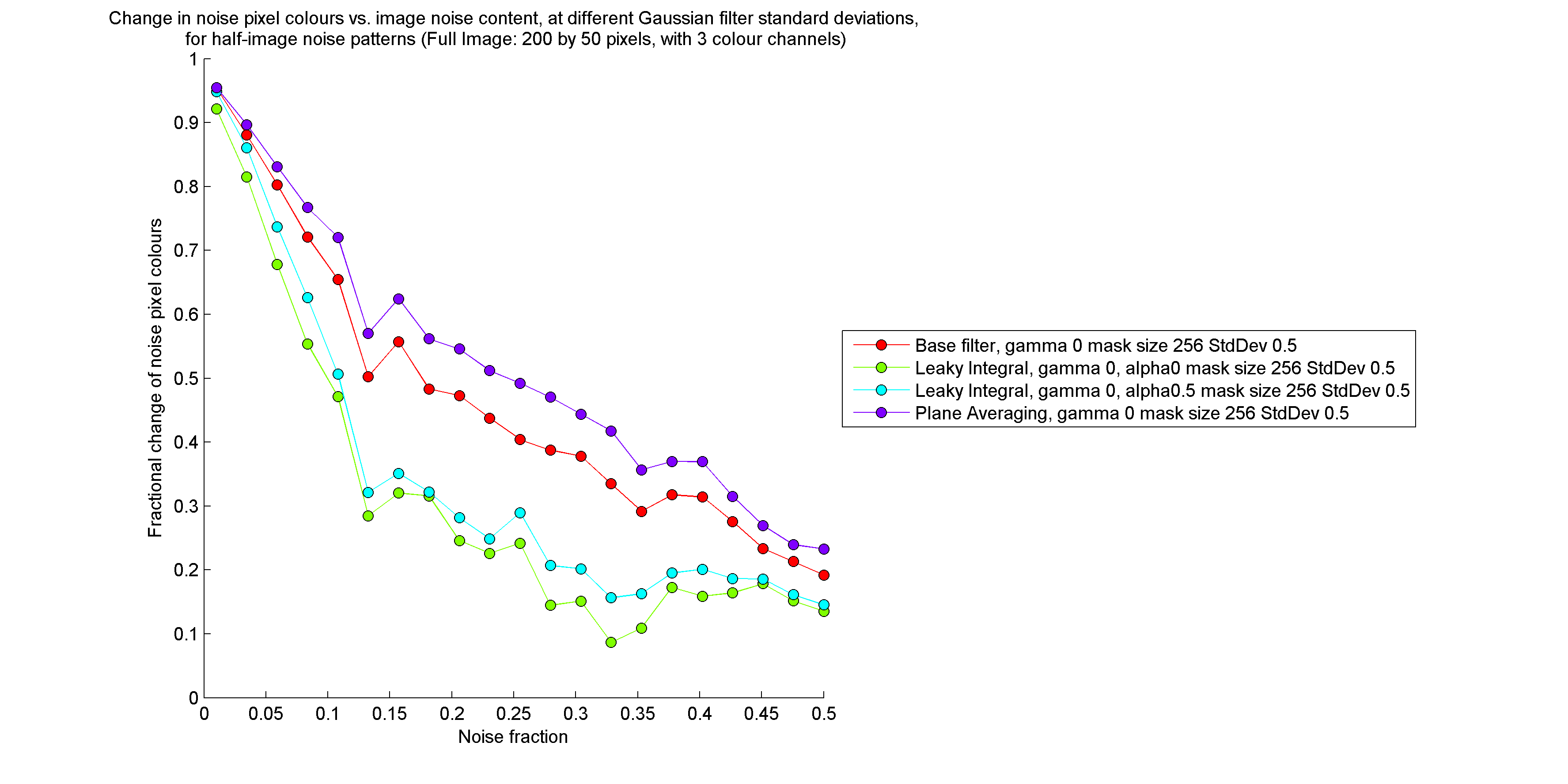
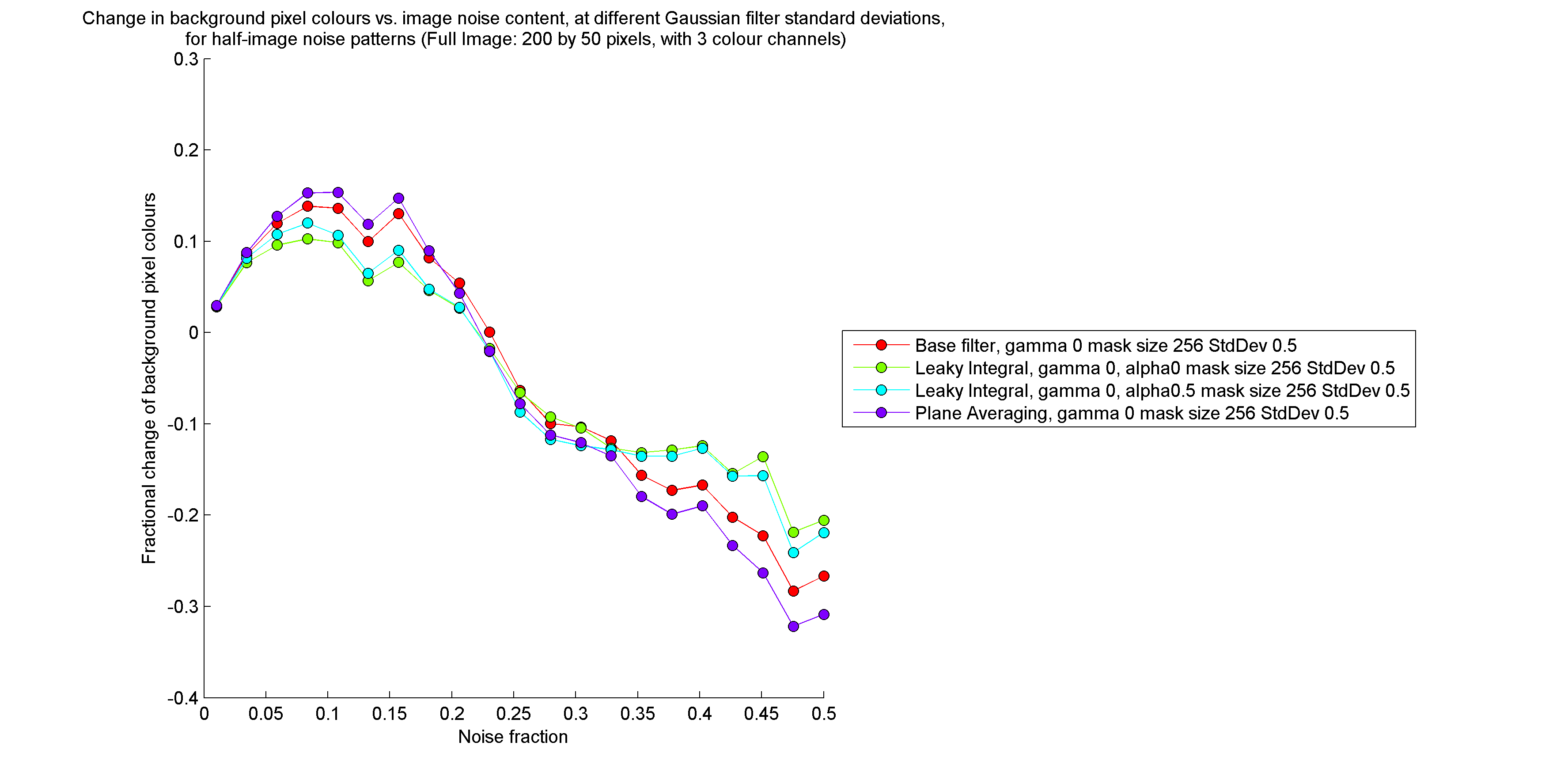
I followed the procedure described at http://gigl.scs.carleton.ca/node/535 for determining how effectively a filter removes outliers from an image. The results are provided below, where the term "plane averaging filter" refers to the filter which fits a plane to the filtering mask of each pixel, and computes new pixel colours by projecting source pixels onto their respective planes. (The plane averaging filter is discussed in detail at http://gigl.scs.carleton.ca/node/522 and http://gigl.scs.carleton.ca/node/537). The "base filter" refers to the normal cumulative range geodesic filter, which is equivalent to the leaky integration filter with an "alpha" value of 1.

Clearly, the leaky integration filter is far less effective at removing noise than both the normal cumulative range geodesic filter and the plane averaging filter. In particular, the leaky integration filter does not suppress noise pixels which occur near to large expanses of the same colour, as shown below. On the other hand, at higher noise contents, the leaky integration filter preserves the colour of the background pixels to a greater extent than the other filters.

In the next post, I will discuss cases where the failure to eliminate outlier colours may actually be beneficial.